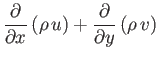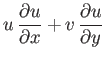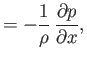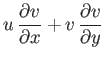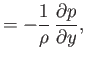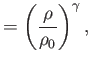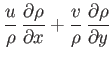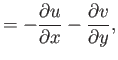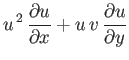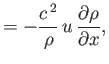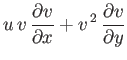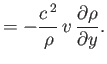

Next: Small-Perturbation Theory
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Crocco's Theorem
Consider a steady, two-dimensional, homenergic, homentropic flow pattern, in the absence of body forces. Suppose that all quantities are independent of the Cartesian coordinate 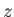 ,
and that the flow velocity,
,
and that the flow velocity, 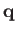 , is confined to the
, is confined to the 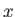 -
-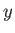 plane. Let
plane. Let
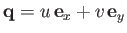 .
Equations (14.25), (14.30), and (14.31) reduce to
.
Equations (14.25), (14.30), and (14.31) reduce to
where 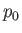 and
and  are the uniform stagnation pressure and density, respectively. (Note that
are the uniform stagnation pressure and density, respectively. (Note that 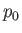 and
and  must be uniform
because the stagnation specific entropy,
must be uniform
because the stagnation specific entropy,
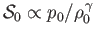 , and the stagnation temperature,
, and the stagnation temperature,
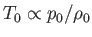 , are both uniform.) Equation (15.95) implies that
, are both uniform.) Equation (15.95) implies that
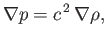 |
(15.96) |
where
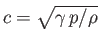 is the sound speed. Hence, Equations (15.92)-(15.94) yield
is the sound speed. Hence, Equations (15.92)-(15.94) yield
Summing the previous two equations, and then making use of Equation (15.97), we obtain
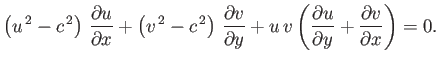 |
(15.100) |
Finally, given that
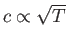 , Equation (14.58) implies that
, Equation (14.58) implies that
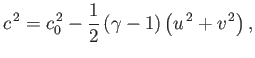 |
(15.101) |
where 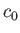 is the stagnation sound speed.
is the stagnation sound speed.


Next: Small-Perturbation Theory
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Crocco's Theorem
Richard Fitzpatrick
2016-03-31