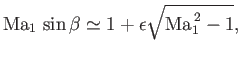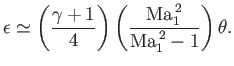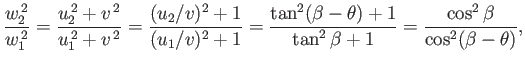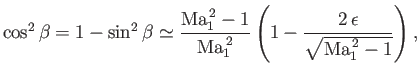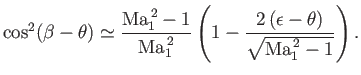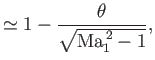Next: Supersonic Compression by Turning
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Supersonic Flow in Corner
Weak Oblique Shocks
For small deflection angles,  , the oblique shock equations reduce to relatively simple expressions. In fact, we already
saw in Equation (15.15) that if
, the oblique shock equations reduce to relatively simple expressions. In fact, we already
saw in Equation (15.15) that if
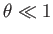 then
then
![$\displaystyle {\rm Ma}_1^{\,2}\,\sin^2\beta-1 \simeq \left[\left(\frac{\gamma+1}{2}\right){\rm Ma}_1^{\,2}\,\tan\beta\right]\theta.$](img5715.png) |
(15.16) |
It follows that 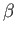 is either close to
is either close to 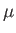 or
or 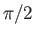 , depending on
whether
, depending on
whether
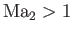 or
or
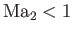 . (See Figure 15.2.)
For the present, we are only considering the former case (
. (See Figure 15.2.)
For the present, we are only considering the former case (
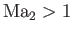 ), for which we may
use the approximation [see Equation (15.6)]
), for which we may
use the approximation [see Equation (15.6)]
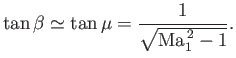 |
(15.17) |
Equation (15.16) then reduces to
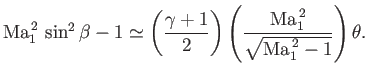 |
(15.18) |
This is the basic relation that is needed to obtain all other approximate expressions, because these expressions only depend on the normal component of the
upstream flow,
 . Thus, Equation (15.1) yields
. Thus, Equation (15.1) yields
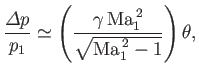 |
(15.19) |
where
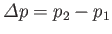 . It is apparent that the shock strength,
. It is apparent that the shock strength,
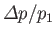 , is directly proportional to the
deflection angle,
, is directly proportional to the
deflection angle,  .
.
The changes in the other flow quantities, except the specific entropy, across the shock front are also directly proportional
to  . (See Exercise iii.) The change in the entropy, on the other hand, is proportional to the third
power of the shock strength (see Section 14.8), and, hence, to the third power of the deflection angle.
. (See Exercise iii.) The change in the entropy, on the other hand, is proportional to the third
power of the shock strength (see Section 14.8), and, hence, to the third power of the deflection angle.
To explicitly find the deviation of the wave angle, 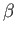 , from the Mach angle,
, from the Mach angle, 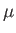 , we write
, we write
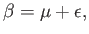 |
(15.20) |
where
 . Thus, we have
. Thus, we have
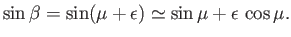 |
(15.21) |
However, by definition,
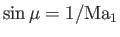 , and
, and
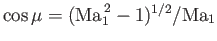 [see Equation (15.6)], so we obtain
[see Equation (15.6)], so we obtain
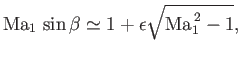 |
(15.22) |
or
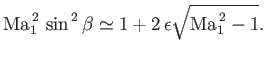 |
(15.23) |
Finally, comparison with Equation (15.18) reveals that
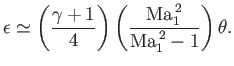 |
(15.24) |
In other words, for a finite deflection angle,  , the wave angle,
, the wave angle, 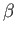 , differs from the Mach angle,
, differs from the Mach angle, 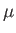 , by an
amount,
, by an
amount,  , that is of the same order of magnitude as
, that is of the same order of magnitude as  .
.
The change in flow speed across the shock front is obtained from the ratio
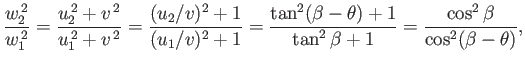 |
(15.25) |
where use has been made of Equations (15.8) and (15.9).
However,
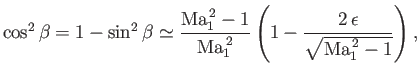 |
(15.26) |
where use has been made of Equation (15.23).
Similarly,
 |
(15.27) |
Hence, to first order in  ,
,
where
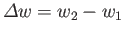 .
.
Figure:
Compression of supersonic flow that is turned through an angle  . Case (a) shows a single turn through an angle
. Case (a) shows a single turn through an angle  .
Case (b) shows the turn subdivided into a number of smaller turns of magnitude
.
Case (b) shows the turn subdivided into a number of smaller turns of magnitude
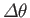 .
Case (c) shows a smooth continuous turn through an angle
.
Case (c) shows a smooth continuous turn through an angle  .
.
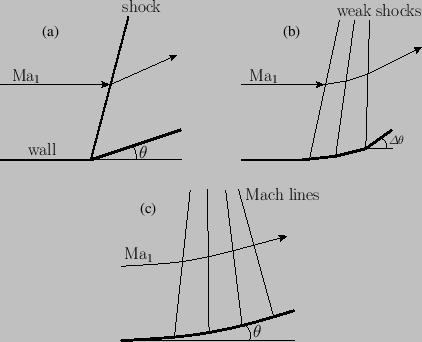 |



Next: Supersonic Compression by Turning
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Supersonic Flow in Corner
Richard Fitzpatrick
2016-03-31
![$\displaystyle {\rm Ma}_1^{\,2}\,\sin^2\beta-1 \simeq \left[\left(\frac{\gamma+1}{2}\right){\rm Ma}_1^{\,2}\,\tan\beta\right]\theta.$](img5715.png)
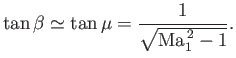
![]() . (See Exercise iii.) The change in the entropy, on the other hand, is proportional to the third
power of the shock strength (see Section 14.8), and, hence, to the third power of the deflection angle.
. (See Exercise iii.) The change in the entropy, on the other hand, is proportional to the third
power of the shock strength (see Section 14.8), and, hence, to the third power of the deflection angle.
![]() , from the Mach angle,
, from the Mach angle, ![]() , we write
, we write