


Next: Supersonic Flow in Corner
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Introduction
Oblique Shocks
Consider a normal shock in which the flow upstream and downstream of the shock front is parallel to the  -axis, and
front itself lies in the
-axis, and
front itself lies in the  -
- plane. (See Section 14.8.) Suppose that
plane. (See Section 14.8.) Suppose that 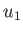 and
and 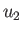 are the upstream and downstream flow speeds, respectively.
Let us now view this shock in a frame of reference that moves with respect to our original frame at the constant velocity
are the upstream and downstream flow speeds, respectively.
Let us now view this shock in a frame of reference that moves with respect to our original frame at the constant velocity
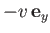 .
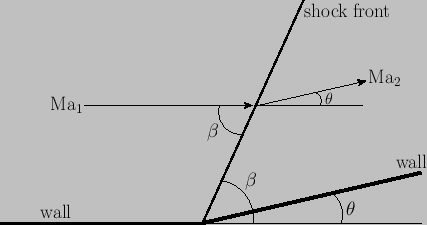
As illustrated in Figure 15.1, viewing the shock in the new reference frame has the effect of adding a component of velocity of magnitude
.
As illustrated in Figure 15.1, viewing the shock in the new reference frame has the effect of adding a component of velocity of magnitude 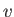 , directed parallel to
the
, directed parallel to
the  -axis, to both the upstream and the downstream flow. The resultant upstream velocity is now of
magnitude
-axis, to both the upstream and the downstream flow. The resultant upstream velocity is now of
magnitude
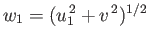 , and subtends an angle
, and subtends an angle
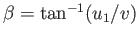 , known as the wave angle, with the shock
front. It is evident that
, known as the wave angle, with the shock
front. It is evident that 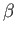 may be adjusted to any value via a suitable choice of
may be adjusted to any value via a suitable choice of 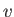 . Now, because
. Now, because 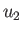 is
not the same as
is
not the same as 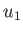 , the inclination of the downstream flow to the shock front is different to that of the
upstream flow. In other words, the direction of the flow turns abruptly as it passes through the shock.
Because
, the inclination of the downstream flow to the shock front is different to that of the
upstream flow. In other words, the direction of the flow turns abruptly as it passes through the shock.
Because 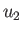 is always less than
is always less than 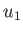 (see Section 14.8), the deviation is always towards the shock front. In other words, the
deflection angle,
(see Section 14.8), the deviation is always towards the shock front. In other words, the
deflection angle,  , defined in Figure 15.1, is positive.
, defined in Figure 15.1, is positive.
Figure 15.1:
An oblique shock.
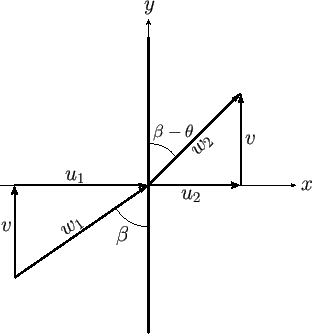 |
The relationship between the conditions upstream and downstream of the shock
is easily obtained from the analysis of Section 14.8, because viewing a
normal shock in a moving frame of reference does not change the relationship
between the upstream and downstream conditions in the original reference frame. The only modification is that the upstream Mach number
is now defined as
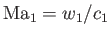 , rather than
, rather than 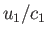 . Here,
. Here,  is the upstream sound speed. Thus, given that
is the upstream sound speed. Thus, given that
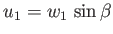 , we simply need to make the transformation
, we simply need to make the transformation
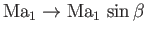 in the previous analysis. Hence, Equations (14.107), (14.108), (14.109),
and (14.113), yield
in the previous analysis. Hence, Equations (14.107), (14.108), (14.109),
and (14.113), yield
respectively. Here, 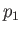 ,
, 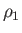 ,
, 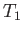 , and
, and
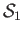 are the upstream pressure, density, temperature, and specific entropy, respectively,
are the upstream pressure, density, temperature, and specific entropy, respectively,
 ,
, 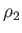 ,
,  , and
, and
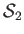 are the corresponding downstream quantities,
are the corresponding downstream quantities, 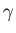 is the ratio of specific heats,
is the ratio of specific heats, 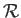 the specific gas constant, and use has been made of Equation (14.59). As before (see Section 14.8), the second law of thermodynamics
demands that
the specific gas constant, and use has been made of Equation (14.59). As before (see Section 14.8), the second law of thermodynamics
demands that
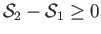 , which implies that
, which implies that
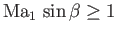 . This sets a minimum inclination
of the upstream flow to the shock front for a given upstream Mach number. The maximum inclination is, of course,
. This sets a minimum inclination
of the upstream flow to the shock front for a given upstream Mach number. The maximum inclination is, of course,
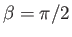 . Thus,
. Thus,
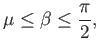 |
(15.5) |
where
 |
(15.6) |
is termed the Mach angle.
The downstream Mach number can be calculated by noting that
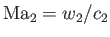 , rather that
, rather that 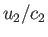 , where
, where 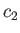 is the downstream sound speed, and
is the downstream sound speed, and
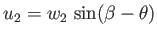 . In other words, we simply need to make the transformation
. In other words, we simply need to make the transformation
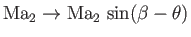 in the
previous analysis.
Thus, it follows from Equation (14.104) that
in the
previous analysis.
Thus, it follows from Equation (14.104) that
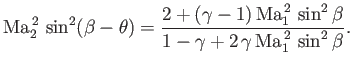 |
(15.7) |
According to Figure 15.1,
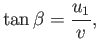 |
(15.8) |
and
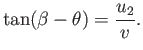 |
(15.9) |
Eliminating 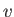 , and then making use of Equation (15.2), we obtain
, and then making use of Equation (15.2), we obtain
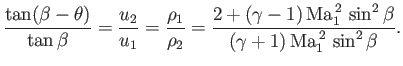 |
(15.10) |
Now,
 |
(15.11) |
so Equation (15.10) can be rearranged to give
![$\displaystyle \tan\theta =\frac{2\,\cot\beta\left({\rm Ma}_1^{\,2}\,\sin^2\beta-1\right)}{2+{\rm Ma}_1^{\,2}\left[\gamma+\cos( 2\,\beta)\right]}.$](img5706.png) |
(15.12) |
Here, use has been made of the identity
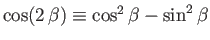 . The previous expression implies that
. The previous expression implies that 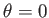 at
at
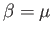 and
and
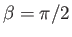 , which are the limits of the range of allowed values for
, which are the limits of the range of allowed values for  defined in Equation (15.5). Within this
range,
defined in Equation (15.5). Within this
range,  is positive, and, must, therefore, have a maximum value,
is positive, and, must, therefore, have a maximum value,
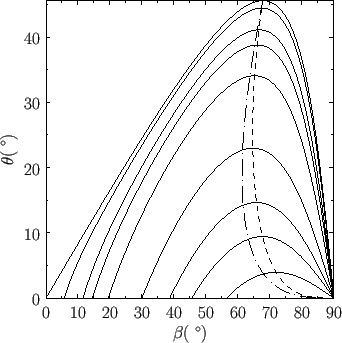
 . This is illustrated in Figure 15.2,
where the relationship between
. This is illustrated in Figure 15.2,
where the relationship between  and
and 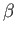 , for an ideal gas with
, for an ideal gas with
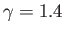 , is plotted for various values of
, is plotted for various values of
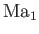 .
.
Figure:
Oblique shock solutions for
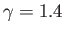 . The solid curves show solutions for
. The solid curves show solutions for
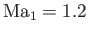 ,
, 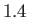 ,
, 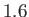 ,
, 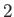 ,
,  ,
, 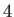 ,
, 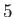 ,
, 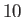 ,
and
,
and 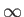 , in order from the innermost to the outermost curve. The dashed curve shows the locus of solutions for which
, in order from the innermost to the outermost curve. The dashed curve shows the locus of solutions for which
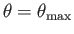 .
The dash-dotted curve shows the locus of solutions for which
.
The dash-dotted curve shows the locus of solutions for which
 . Solutions to the left and
right of the dash-dotted curve correspond to
. Solutions to the left and
right of the dash-dotted curve correspond to
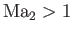 and
and
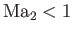 , respectively.
, respectively.
 |
If
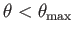 then, for each value of
then, for each value of  and
and
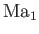 , there are two possible solutions, corresponding to two
different values of
, there are two possible solutions, corresponding to two
different values of 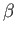 . The larger value of
. The larger value of 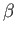 corresponds to the stronger shock [because, according to Equation (15.1), the shock strength,
corresponds to the stronger shock [because, according to Equation (15.1), the shock strength,  , is a
monotonically increasing function of
, is a
monotonically increasing function of 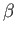 ].
].
Also shown in Figure 15.2 is the locus of solutions for which
 .
In the solution with the stronger shock, the downstream flow always becomes subsonic. On the other hand, in the
solution with the weaker shock, the downstream flow remains supersonic, except for a small range of
values of
.
In the solution with the stronger shock, the downstream flow always becomes subsonic. On the other hand, in the
solution with the weaker shock, the downstream flow remains supersonic, except for a small range of
values of  that are slightly smaller that
that are slightly smaller that
 .
.
Equation (15.10) can be rearranged to give
 |
(15.13) |
which can be further reduced to
 |
(15.14) |
For small deflection angles,  , the previous expression can be approximated by
, the previous expression can be approximated by
![$\displaystyle {\rm Ma}_1^{\,2}\,\sin^2\beta-1 \simeq \left[\left(\frac{\gamma+1}{2}\right){\rm Ma}_1^{\,2}\,\tan\beta\right]\theta.$](img5715.png) |
(15.15) |
Figure 15.3:
Supersonic flow in concave corner.
 |



Next: Supersonic Flow in Corner
Up: Two-Dimensional Compressible Inviscid Flow
Previous: Introduction
Richard Fitzpatrick
2016-03-31
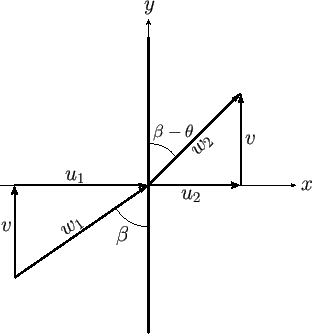
![]() , rather than
, rather than ![]() . Here,
. Here, ![]() is the upstream sound speed. Thus, given that
is the upstream sound speed. Thus, given that
![]() , we simply need to make the transformation
, we simply need to make the transformation
![]() in the previous analysis. Hence, Equations (14.107), (14.108), (14.109),
and (14.113), yield
in the previous analysis. Hence, Equations (14.107), (14.108), (14.109),
and (14.113), yield


![]() then, for each value of
then, for each value of ![]() and
and
![]() , there are two possible solutions, corresponding to two
different values of
, there are two possible solutions, corresponding to two
different values of ![]() . The larger value of
. The larger value of ![]() corresponds to the stronger shock [because, according to Equation (15.1), the shock strength,
corresponds to the stronger shock [because, according to Equation (15.1), the shock strength, ![]() , is a
monotonically increasing function of
, is a
monotonically increasing function of ![]() ].
].
![]() .
In the solution with the stronger shock, the downstream flow always becomes subsonic. On the other hand, in the
solution with the weaker shock, the downstream flow remains supersonic, except for a small range of
values of
.
In the solution with the stronger shock, the downstream flow always becomes subsonic. On the other hand, in the
solution with the weaker shock, the downstream flow remains supersonic, except for a small range of
values of ![]() that are slightly smaller that
that are slightly smaller that
![]() .
.

