The wall deflection can be subdivided into several segments, which make
smaller corners of angle
![]() , as shown in Figure 15.6(b).
Compression then occurs through successive oblique shocks. These shocks divide the flow
field close to the wall into segments of uniform flow. Further out, the shocks must
intersect one another, because they are convergent. However, for the present, we shall only
consider the flow close to the wall. In this region, each segment of the flow is
independent of the following segment. In other words, the flow pattern can be constructed step by step, proceeding downstream.
This property of limited upstream influence exists as long as the deflection does not become so large that the flow
is rendered subsonic.
, as shown in Figure 15.6(b).
Compression then occurs through successive oblique shocks. These shocks divide the flow
field close to the wall into segments of uniform flow. Further out, the shocks must
intersect one another, because they are convergent. However, for the present, we shall only
consider the flow close to the wall. In this region, each segment of the flow is
independent of the following segment. In other words, the flow pattern can be constructed step by step, proceeding downstream.
This property of limited upstream influence exists as long as the deflection does not become so large that the flow
is rendered subsonic.
To compare the compression in the two cases, (a) and (b), of Figure 15.6, we shall make use of the approximate expressions for weak shocks obtained in the preceding section. For each shock in case (b), we have
| (15.30) | ||
| (15.31) |
| (15.32) |
| (15.33) | ||
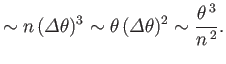 |
(15.34) |
In the limit that
![]() , the smooth turn of Figure 15.6(c) is obtained.
In this case, the net increase in specific entropy becomes vanishingly small. In other words, the
compression becomes isentropic.
We can also deduce the following results. First, the shocks become vanishingly weak, their limiting
positions being straight Mach lines emanating from the wall. Second, each segment of uniform flow becomes vanishingly narrow,
and eventually coincides with a Mach line. Thus, on each Mach line, both the flow inclination and the Mach number are
constant. Third, the limited upstream influence is preserved. That is, the flow upstream of a given Mach line is not affected by any downstream modifications in the
wall. Finally, the approximate expression for the change in flow speed across a weak shock, Equation (15.29), becomes the
differential expression
, the smooth turn of Figure 15.6(c) is obtained.
In this case, the net increase in specific entropy becomes vanishingly small. In other words, the
compression becomes isentropic.
We can also deduce the following results. First, the shocks become vanishingly weak, their limiting
positions being straight Mach lines emanating from the wall. Second, each segment of uniform flow becomes vanishingly narrow,
and eventually coincides with a Mach line. Thus, on each Mach line, both the flow inclination and the Mach number are
constant. Third, the limited upstream influence is preserved. That is, the flow upstream of a given Mach line is not affected by any downstream modifications in the
wall. Finally, the approximate expression for the change in flow speed across a weak shock, Equation (15.29), becomes the
differential expression
Let us now consider what happens to the flow further away from the wall, where the weak shocks and
Mach lines of Figure 15.6(b) and Figure 15.6(c), respectively, converge. Consider Figure 15.7.
Because of the convergence of the Mach lines, the change from the initial Mach number,
![]() , to the final
Mach number,
, to the final
Mach number,
![]() , is achieved in a
much shorter distance on streamline
, is achieved in a
much shorter distance on streamline ![]() than on streamline
than on streamline ![]() . Thus, the velocity gradients on streamline
. Thus, the velocity gradients on streamline ![]() are higher than those on streamline
are higher than those on streamline ![]() . Now, an intersection of
Mach lines would imply infinitely high velocity gradients, because there would be two different values of the Mach number at a single point.
In practice, this does not occur, because, in the region where the Mach lines converge, and before they cross, the
velocity gradients become high enough that the conditions are no longer isentropic. In fact, a shock wave develops, as
illustrated in the figure.
. Now, an intersection of
Mach lines would imply infinitely high velocity gradients, because there would be two different values of the Mach number at a single point.
In practice, this does not occur, because, in the region where the Mach lines converge, and before they cross, the
velocity gradients become high enough that the conditions are no longer isentropic. In fact, a shock wave develops, as
illustrated in the figure.