Square Potential Barrier
Consider a particle of mass  and energy
and energy  interacting with the
simple, one-dimensional, potential barrier
interacting with the
simple, one-dimensional, potential barrier
![$\displaystyle U(x) = \left\{\begin{array}{rcl}
V&\mbox{\hspace{1cm}}&\mbox{for $0\leq x\leq a$}\\ [0.5ex]
0&&\mbox{otherwise}
\end{array}\right.,$](img4002.png) |
(11.93) |
where  . In the regions to the left and to the right of the
barrier, the stationary wavefunction,
. In the regions to the left and to the right of the
barrier, the stationary wavefunction, 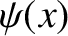 , satisfies
, satisfies
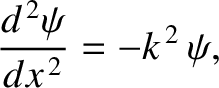 |
(11.94) |
where
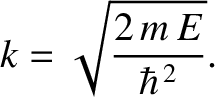 |
(11.95) |
Let us adopt the following solution
of the previous equation to the left of the barrier (i.e., 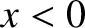 ):
):
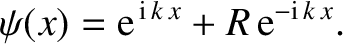 |
(11.96) |
This solution consists of a plane wave of unit amplitude traveling to
the right [because the full wavefunction is multiplied by a factor
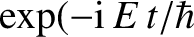 )], and a plane wave of complex amplitude
)], and a plane wave of complex amplitude  traveling to
the left. We interpret the first plane wave as an incident particle, and
the second as a particle reflected by the potential barrier. Hence,
traveling to
the left. We interpret the first plane wave as an incident particle, and
the second as a particle reflected by the potential barrier. Hence, 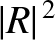 is
the probability of reflection. (See Sections 6.7 and 11.6.)
is
the probability of reflection. (See Sections 6.7 and 11.6.)
Let us adopt the following solution to Equation (11.94) to the right
of the barrier (i.e. 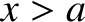 ):
):
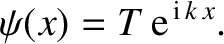 |
(11.97) |
This solution consists of a plane wave of complex amplitude  traveling to the right. We interpret the plane wave as a particle transmitted through
the barrier. Hence,
traveling to the right. We interpret the plane wave as a particle transmitted through
the barrier. Hence, 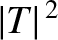 is the probability of transmission.
is the probability of transmission.
Let us, first of all, consider the situation in which 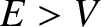 . In this case, according to classical mechanics, the
particle slows down as it passes through the barrier, but is otherwise unaffected. In other words, the
classical probability of reflection is zero, and the classical probability of transmission is unity. However,
this is not necessarily the case in wave mechanics. In fact, inside the barrier (i.e.,
. In this case, according to classical mechanics, the
particle slows down as it passes through the barrier, but is otherwise unaffected. In other words, the
classical probability of reflection is zero, and the classical probability of transmission is unity. However,
this is not necessarily the case in wave mechanics. In fact, inside the barrier (i.e.,
 ),
), 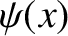 satisfies
satisfies
 |
(11.98) |
where
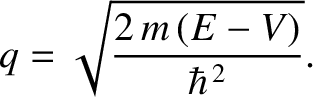 |
(11.99) |
The general solution to Equation (11.98) takes the form
 |
(11.100) |
Continuity of 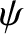 and
and 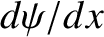 at the left edge of
the barrier (i.e.,
at the left edge of
the barrier (i.e.,  ) yields
Likewise, continuity of
) yields
Likewise, continuity of  and
and 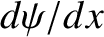 at the right edge of
the barrier (i.e.,
at the right edge of
the barrier (i.e.,  ) gives
After considerable algebra, the previous four equations yield
) gives
After considerable algebra, the previous four equations yield
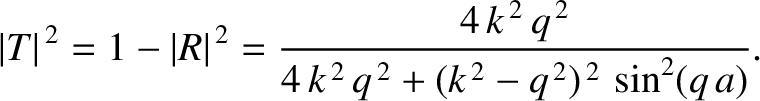 |
(11.105) |
The fact that
 ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
Figure: 11.8
Transmission (solid curve) and reflection (dashed curve) probabilities for a square potential barrier of width
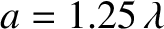 , where
, where  is the free-space de Broglie wavelength, as a function
of the ratio of the height of the barrier,
is the free-space de Broglie wavelength, as a function
of the ratio of the height of the barrier, 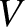 , to the
energy,
, to the
energy,  , of the incident particle.
, of the incident particle.
|
|
Figure 11.9:
Transmission (solid curve) and reflection (dashed curve) probabilities for a particle of energy  incident on a square potential barrier of height
incident on a square potential barrier of height
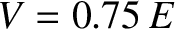 as a function
of the ratio of the width of the barrier,
as a function
of the ratio of the width of the barrier, 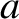 , to the free-space de Broglie
wavelength,
, to the free-space de Broglie
wavelength,  .
.
|
|
The reflection and transmission probabilities obtained from Equation (11.105) are plotted in Figures 11.8 and
11.9. It can be seen, from Figure 11.8, that the classical
result,
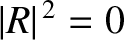 and
and
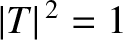 , is obtained in the limit where the height of the barrier
is relatively small (i.e.,
, is obtained in the limit where the height of the barrier
is relatively small (i.e.,  ). However, if
). However, if 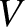 is
of order
is
of order  then there is a substantial probability that the incident particle
will be reflected by the barrier. According to classical physics, reflection is impossible when
then there is a substantial probability that the incident particle
will be reflected by the barrier. According to classical physics, reflection is impossible when 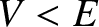 .
.
It can also be seen, from Figure 11.9,
that at certain barrier widths the probability of reflection goes to zero. It turns out that this is true irrespective of the energy of the incident particle.
It is evident, from Equation (11.105), that these special barrier widths
correspond to
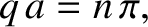 |
(11.106) |
where
 . In other words, the special barrier widths are
integer multiples of half the de Broglie wavelength of the particle inside the
barrier. There is no reflection at the special barrier widths because, at these
widths,
the backward traveling wave reflected from the left edge of the barrier
interferes destructively with the similar wave reflected from the right
edge of the barrier to give zero net reflected wave. (See Section 6.7.)
. In other words, the special barrier widths are
integer multiples of half the de Broglie wavelength of the particle inside the
barrier. There is no reflection at the special barrier widths because, at these
widths,
the backward traveling wave reflected from the left edge of the barrier
interferes destructively with the similar wave reflected from the right
edge of the barrier to give zero net reflected wave. (See Section 6.7.)
Let us now consider the situation in which 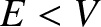 . In this case, according to classical mechanics, the particle is
unable to penetrate the barrier, so the coefficient of reflection is unity, and the coefficient
of transmission zero.
However, this is not necessarily the case in wave mechanics.
In fact, inside the barrier (i.e.,
. In this case, according to classical mechanics, the particle is
unable to penetrate the barrier, so the coefficient of reflection is unity, and the coefficient
of transmission zero.
However, this is not necessarily the case in wave mechanics.
In fact, inside the barrier (i.e.,
 ),
), 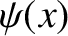 satisfies
satisfies
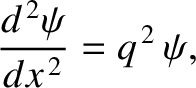 |
(11.107) |
where
 |
(11.108) |
The general
solution to Equation (11.107) takes the
form
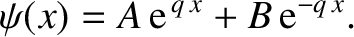 |
(11.109) |
Continuity of 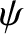 and
and
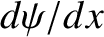 at the left edge of
the barrier (i.e.,
at the left edge of
the barrier (i.e.,  ) yields
Likewise, continuity of
) yields
Likewise, continuity of 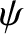 and
and 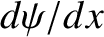 at the right edge of
the barrier (i.e.,
at the right edge of
the barrier (i.e.,  ) gives
After considerable algebra, the preceding four equations yield
) gives
After considerable algebra, the preceding four equations yield
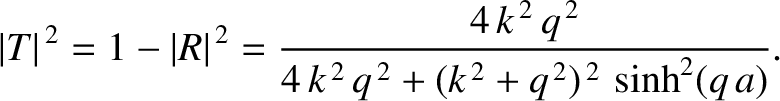 |
(11.114) |
The fact that
 again ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
again ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
Figure: 11.10
Transmission (solid curve) and reflection (dashed curve) probabilities for a square potential barrier of width
 , where
, where  is the free-space de Broglie wavelength, as a function
of the ratio of the energy,
is the free-space de Broglie wavelength, as a function
of the ratio of the energy,  , of the incoming particle to the
height,
, of the incoming particle to the
height, 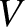 , of the barrier.
, of the barrier.
|
|
Figure 11.11:
Transmission (solid curve) and reflection (dashed curve) probabilities for a particle of energy  incident on a square potential barrier of height
incident on a square potential barrier of height
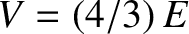 as a function
of the ratio of the width of the barrier,
as a function
of the ratio of the width of the barrier, 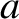 , to the free-space de Broglie
wavelength,
, to the free-space de Broglie
wavelength,  .
.
|
|
The reflection and transmission probabilities obtained from Equation (11.114) are plotted in Figures 11.10 and
11.11. It can be seen, from these two figures, that the classical
result,
 and
and
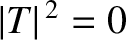 , is obtained for relatively
thin barriers (i.e.,
, is obtained for relatively
thin barriers (i.e.,
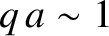 ) in the limit where the height of the barrier
is relatively large (i.e.,
) in the limit where the height of the barrier
is relatively large (i.e.,  ). However, if
). However, if 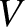 is
of order
is
of order  then there is a substantial probability that the incident particle
will be transmitted by the barrier. According to classical physics, transmission is impossible when
then there is a substantial probability that the incident particle
will be transmitted by the barrier. According to classical physics, transmission is impossible when 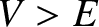 .
.
It can also be seen, from
Figure 11.11, that the transmission probability decays exponentially
as the width of the barrier increases. Nevertheless, even for very
wide barriers (i.e., 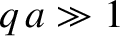 ), there is a small but finite
probability that a particle incident on the barrier will be
transmitted. This phenomenon, which is inexplicable within
the context of classical physics, is called tunneling.
For the case of a very high barrier, such that
), there is a small but finite
probability that a particle incident on the barrier will be
transmitted. This phenomenon, which is inexplicable within
the context of classical physics, is called tunneling.
For the case of a very high barrier, such that
 , the tunneling probability reduces to
, the tunneling probability reduces to
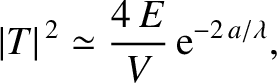 |
(11.115) |
where
 is the de Broglie wavelength inside the barrier. Here, it
is assumed that
is the de Broglie wavelength inside the barrier. Here, it
is assumed that
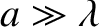 .
Thus, even in the limit that the barrier is very high, there is an exponentially small, but nevertheless non-zero, tunneling probability.
Quantum mechanical tunneling plays an important role in the physics
of electron field emission and
.
Thus, even in the limit that the barrier is very high, there is an exponentially small, but nevertheless non-zero, tunneling probability.
Quantum mechanical tunneling plays an important role in the physics
of electron field emission and  -decay (Park 1974). (See Sections 11.14 and 11.15.)
-decay (Park 1974). (See Sections 11.14 and 11.15.)
 and energy
and energy  interacting with the
simple, one-dimensional, potential barrier
interacting with the
simple, one-dimensional, potential barrier
![$\displaystyle U(x) = \left\{\begin{array}{rcl}
V&\mbox{\hspace{1cm}}&\mbox{for $0\leq x\leq a$}\\ [0.5ex]
0&&\mbox{otherwise}
\end{array}\right.,$](img4002.png)
 . In the regions to the left and to the right of the
barrier, the stationary wavefunction,
. In the regions to the left and to the right of the
barrier, the stationary wavefunction, 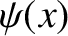 , satisfies
where
, satisfies
where
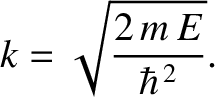
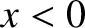 ):
):
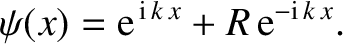
 )], and a plane wave of complex amplitude
)], and a plane wave of complex amplitude  traveling to
the left. We interpret the first plane wave as an incident particle, and
the second as a particle reflected by the potential barrier. Hence,
traveling to
the left. We interpret the first plane wave as an incident particle, and
the second as a particle reflected by the potential barrier. Hence, 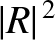 is
the probability of reflection. (See Sections 6.7 and 11.6.)
is
the probability of reflection. (See Sections 6.7 and 11.6.)
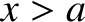 ):
):
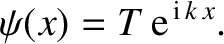
 traveling to the right. We interpret the plane wave as a particle transmitted through
the barrier. Hence,
traveling to the right. We interpret the plane wave as a particle transmitted through
the barrier. Hence, 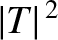 is the probability of transmission.
is the probability of transmission.
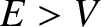 . In this case, according to classical mechanics, the
particle slows down as it passes through the barrier, but is otherwise unaffected. In other words, the
classical probability of reflection is zero, and the classical probability of transmission is unity. However,
this is not necessarily the case in wave mechanics. In fact, inside the barrier (i.e.,
. In this case, according to classical mechanics, the
particle slows down as it passes through the barrier, but is otherwise unaffected. In other words, the
classical probability of reflection is zero, and the classical probability of transmission is unity. However,
this is not necessarily the case in wave mechanics. In fact, inside the barrier (i.e.,
 ),
), 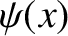 satisfies
satisfies
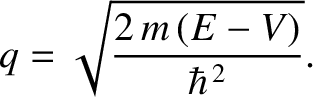

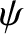 and
and 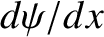 at the left edge of
the barrier (i.e.,
at the left edge of
the barrier (i.e.,  ) yields
) yields
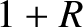
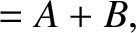
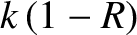

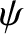 and
and 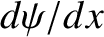 at the right edge of
the barrier (i.e.,
at the right edge of
the barrier (i.e.,  ) gives
) gives
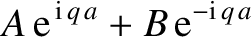
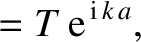
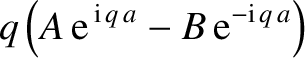
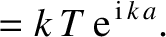
 ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
![\includegraphics[width=0.85\textwidth]{Chapter11/fig11_08.eps}](img4025.png)
![\includegraphics[width=0.85\textwidth]{Chapter11/fig11_09.eps}](img4027.png)
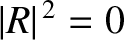 and
and
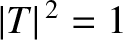 , is obtained in the limit where the height of the barrier
is relatively small (i.e.,
, is obtained in the limit where the height of the barrier
is relatively small (i.e.,  ). However, if
). However, if 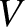 is
of order
is
of order  then there is a substantial probability that the incident particle
will be reflected by the barrier. According to classical physics, reflection is impossible when
then there is a substantial probability that the incident particle
will be reflected by the barrier. According to classical physics, reflection is impossible when 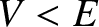 .
.
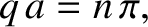
 . In other words, the special barrier widths are
integer multiples of half the de Broglie wavelength of the particle inside the
barrier. There is no reflection at the special barrier widths because, at these
widths,
the backward traveling wave reflected from the left edge of the barrier
interferes destructively with the similar wave reflected from the right
edge of the barrier to give zero net reflected wave. (See Section 6.7.)
. In other words, the special barrier widths are
integer multiples of half the de Broglie wavelength of the particle inside the
barrier. There is no reflection at the special barrier widths because, at these
widths,
the backward traveling wave reflected from the left edge of the barrier
interferes destructively with the similar wave reflected from the right
edge of the barrier to give zero net reflected wave. (See Section 6.7.)
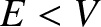 . In this case, according to classical mechanics, the particle is
unable to penetrate the barrier, so the coefficient of reflection is unity, and the coefficient
of transmission zero.
However, this is not necessarily the case in wave mechanics.
In fact, inside the barrier (i.e.,
. In this case, according to classical mechanics, the particle is
unable to penetrate the barrier, so the coefficient of reflection is unity, and the coefficient
of transmission zero.
However, this is not necessarily the case in wave mechanics.
In fact, inside the barrier (i.e.,
 ),
), 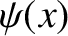 satisfies
satisfies

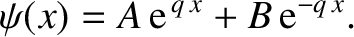
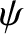 and
and
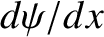 at the left edge of
the barrier (i.e.,
at the left edge of
the barrier (i.e.,  ) yields
) yields
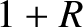
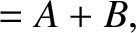


 and
and  at the right edge of
the barrier (i.e.,
at the right edge of
the barrier (i.e.,  ) gives
) gives
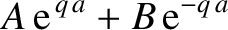
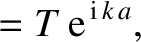
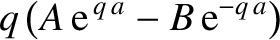
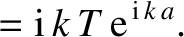
 again ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
again ensures that the probabilities of reflection and
transmission sum to unity, as must be the case, because reflection and transmission
are the only possible outcomes for a particle incident on the barrier.
![\includegraphics[width=0.85\textwidth]{Chapter11/fig11_10.eps}](img4044.png)
![\includegraphics[width=0.85\textwidth]{Chapter11/fig11_11.eps}](img4046.png)
 and
and
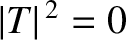 , is obtained for relatively
thin barriers (i.e.,
, is obtained for relatively
thin barriers (i.e.,
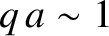 ) in the limit where the height of the barrier
is relatively large (i.e.,
) in the limit where the height of the barrier
is relatively large (i.e.,  ). However, if
). However, if 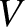 is
of order
is
of order  then there is a substantial probability that the incident particle
will be transmitted by the barrier. According to classical physics, transmission is impossible when
then there is a substantial probability that the incident particle
will be transmitted by the barrier. According to classical physics, transmission is impossible when 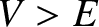 .
.
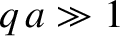 ), there is a small but finite
probability that a particle incident on the barrier will be
transmitted. This phenomenon, which is inexplicable within
the context of classical physics, is called tunneling.
For the case of a very high barrier, such that
), there is a small but finite
probability that a particle incident on the barrier will be
transmitted. This phenomenon, which is inexplicable within
the context of classical physics, is called tunneling.
For the case of a very high barrier, such that
 , the tunneling probability reduces to
, the tunneling probability reduces to
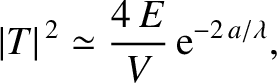
 is the de Broglie wavelength inside the barrier. Here, it
is assumed that
is the de Broglie wavelength inside the barrier. Here, it
is assumed that
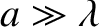 .
Thus, even in the limit that the barrier is very high, there is an exponentially small, but nevertheless non-zero, tunneling probability.
Quantum mechanical tunneling plays an important role in the physics
of electron field emission and
.
Thus, even in the limit that the barrier is very high, there is an exponentially small, but nevertheless non-zero, tunneling probability.
Quantum mechanical tunneling plays an important role in the physics
of electron field emission and  -decay (Park 1974). (See Sections 11.14 and 11.15.)
-decay (Park 1974). (See Sections 11.14 and 11.15.)