Next: Cold Emission Up: Wave Mechanics Previous: Square Potential Barrier Contents
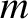 and energy
and energy 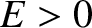 moving through some slowly-varying
potential,
moving through some slowly-varying
potential, 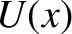 . The particle's wavefunction satisfies
where
. The particle's wavefunction satisfies
where
![$\displaystyle k^{\,2}(x) = \frac{2\,m\,[E-U(x)]}{\hbar^2}.$](img4058.png) |
(11.117) |
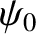 is a complex constant. Note that this solution represents
a particle propagating in the positive
is a complex constant. Note that this solution represents
a particle propagating in the positive  -direction [because the full
wavefunction is multiplied by
-direction [because the full
wavefunction is multiplied by
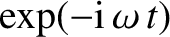 , where
, where
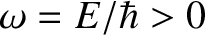 ] with the continuously-varying wavenumber
] with the continuously-varying wavenumber
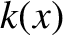 .
It follows that
.
It follows that
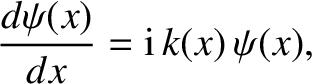 |
(11.119) |
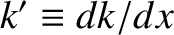 . A comparison of Equations (11.116) and (11.120)
reveals that Equation (11.118) represents an approximate solution to
Equation (11.116) provided that the first term on the right-hand side of Equation (11.120)
is negligible compared to the second. This yields
the validity criterion
. A comparison of Equations (11.116) and (11.120)
reveals that Equation (11.118) represents an approximate solution to
Equation (11.116) provided that the first term on the right-hand side of Equation (11.120)
is negligible compared to the second. This yields
the validity criterion
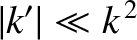 , or
In other words, the variation lengthscale of
, or
In other words, the variation lengthscale of 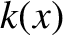 , which is
approximately the same as the variation lengthscale of
, which is
approximately the same as the variation lengthscale of 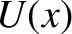 , must
be much greater than the particle's de Broglie wavelength (which
is of order
, must
be much greater than the particle's de Broglie wavelength (which
is of order 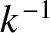 ). Let us suppose that this is the case. Incidentally,
the approximation involved in dropping the first term on the right-hand side
of Equation (11.120) is generally known as the WKB approximation, after G. Wentzel, H.A. Kramers, and L. Brillouin. (See Section 6.10.)
Similarly, Equation (11.118) is termed a WKB solution.
). Let us suppose that this is the case. Incidentally,
the approximation involved in dropping the first term on the right-hand side
of Equation (11.120) is generally known as the WKB approximation, after G. Wentzel, H.A. Kramers, and L. Brillouin. (See Section 6.10.)
Similarly, Equation (11.118) is termed a WKB solution.
According to the WKB solution, (11.118), the probability density remains constant; that is,
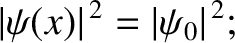 |
(11.122) |
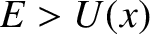 , and
, and 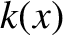 is consequently real (i.e., an allowed region
according to classical physics).
Suppose, however, that the particle encounters a potential barrier (i.e., a region from which the particle is excluded according to classical
physics). By definition,
is consequently real (i.e., an allowed region
according to classical physics).
Suppose, however, that the particle encounters a potential barrier (i.e., a region from which the particle is excluded according to classical
physics). By definition, 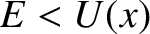 inside such a barrier, and
inside such a barrier, and
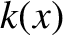 is consequently imaginary. Let the barrier extend from
is consequently imaginary. Let the barrier extend from 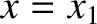 to
to 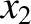 , where
, where
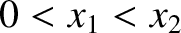 . The WKB solution inside the barrier is written
where
. The WKB solution inside the barrier is written
where
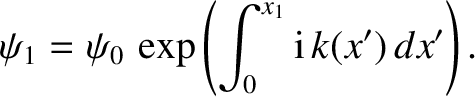 |
(11.124) |
According to the WKB solution, (11.123), the probability density decays exponentially inside the barrier; that is,
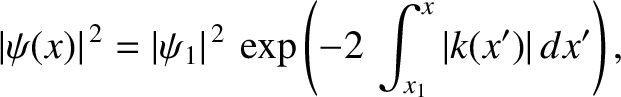 |
(11.125) |
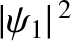 is the probability density at the left-hand
side of the barrier (i.e.,
is the probability density at the left-hand
side of the barrier (i.e., 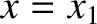 ). It follows that the
probability density at the right-hand side of the barrier (i.e.,
). It follows that the
probability density at the right-hand side of the barrier (i.e., 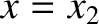 ) is
) is
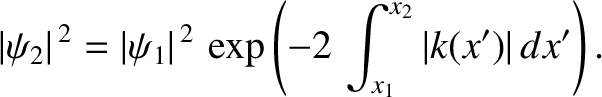 |
(11.126) |
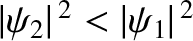 . Of course, in the region to the right of the
barrier (i.e.,
. Of course, in the region to the right of the
barrier (i.e., 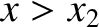 ), the probability density takes the
constant value
), the probability density takes the
constant value
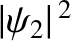 .
.
We can interpret the ratio of the probability densities to the right and to the left of the potential barrier as the probability, 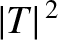 , that a particle
incident from the left will tunnel through the barrier and
emerge on the other side; that is,
, that a particle
incident from the left will tunnel through the barrier and
emerge on the other side; that is,
Note that the criterion (11.121) for the validity of the WKB approximation
implies that the previous transmission probability is very small. Hence,
the WKB approximation only applies to situations in which there is
very little chance of a particle tunneling through the potential barrier in question.
Unfortunately, the validity criterion (11.121) breaks down completely
at the edges of the barrier (i.e., at 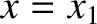 and
and 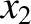 ), because
), because
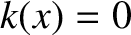 at these points. However, it can be demonstrated that the
contribution of those regions, around
at these points. However, it can be demonstrated that the
contribution of those regions, around 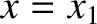 and
and 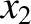 , in which the WKB
approximation breaks down to the integral in Equation (11.127)
is fairly negligible (Schiff 1955). Hence, the previous expression for the tunneling
probability is a reasonable approximation provided that the incident particle's
de Broglie wavelength is much smaller than the spatial extent of the potential
barrier.
, in which the WKB
approximation breaks down to the integral in Equation (11.127)
is fairly negligible (Schiff 1955). Hence, the previous expression for the tunneling
probability is a reasonable approximation provided that the incident particle's
de Broglie wavelength is much smaller than the spatial extent of the potential
barrier.