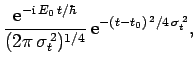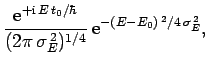Next: Eigenstates and Eigenvalues
Up: Fundamentals of Quantum Mechanics
Previous: Momentum Representation
Heisenberg's Uncertainty Principle
Consider a real-space Hermitian operator 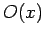 . A straightforward generalization of Eq. (193) yields
. A straightforward generalization of Eq. (193) yields
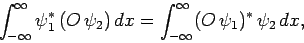 |
(222) |
where  and
and 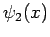 are general functions.
are general functions.
Let
 , where
, where 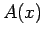 is an Hermitian operator,
and
is an Hermitian operator,
and 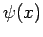 a general wavefunction. We have
a general wavefunction. We have
![\begin{displaymath}
\int_{-\infty}^\infty \vert f\vert^{ 2} dx= \int_{-\infty}...
...e A\rangle) \psi]^{ \ast} [(A-\langle A\rangle) \psi] dx.
\end{displaymath}](img607.png) |
(223) |
Making use of Eq. (222), we obtain
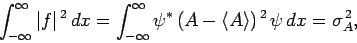 |
(224) |
where
 is the variance of
is the variance of  [see Eq. (160)].
Similarly, if
[see Eq. (160)].
Similarly, if
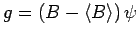 , where
, where  is a second
Hermitian operator, then
is a second
Hermitian operator, then
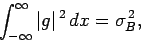 |
(225) |
Now, there is a standard result in mathematics, known as the
Schwartz inequality, which states that
 |
(226) |
where  and
and 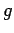 are two general functions. Furthermore, if
are two general functions. Furthermore, if 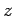 is
a complex number then
is
a complex number then
![\begin{displaymath}
\vert z\vert^{ 2} = [{\rm Re}(z)]^{ 2} + [{\rm Im}(z)]^{ ...
...]^{ 2} = \left[\frac{1}{2 {\rm i}} (z-z^\ast)\right]^{ 2}.
\end{displaymath}](img614.png) |
(227) |
Hence, if
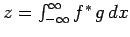 then Eqs. (224)-(227) yield
then Eqs. (224)-(227) yield
![\begin{displaymath}
\sigma_A^{ 2} \sigma_B^{ 2} \geq \left[\frac{1}{2 {\rm i}} (z-z^\ast)\right]^{ 2}.
\end{displaymath}](img616.png) |
(228) |
However,
![\begin{displaymath}
z = \int_{-\infty}^{\infty} [(A-\langle A\rangle) \psi]^{ ...
...si^\ast (A-\langle A\rangle) (B-\langle B\rangle) \psi dx,
\end{displaymath}](img617.png) |
(229) |
where use has been made of Eq. (222). The above
equation reduces to
 |
(230) |
Furthermore, it is easily demonstrated that
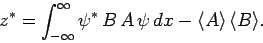 |
(231) |
Hence, Eq. (228) gives
![\begin{displaymath}
\sigma_A^{ 2} \sigma_B^{ 2} \geq \left(\frac{1}{2 {\rm i}}\langle[A,B]\rangle\right)^{ 2},
\end{displaymath}](img620.png) |
(232) |
where
![\begin{displaymath}[A,B]\equiv A B-B A.
\end{displaymath}](img621.png) |
(233) |
Equation (232) is the general form of Heisenberg's uncertainty principle in quantum mechanics. It states that if two dynamical
variables are represented by the two Hermitian operators  and
and  ,
and these operators do not commute (i.e.,
,
and these operators do not commute (i.e.,  ),
then it is impossible to simultaneously (exactly) measure the two variables.
Instead, the product of the variances in the measurements is always greater than some critical value, which
depends on the extent to which the two operators do not commute.
),
then it is impossible to simultaneously (exactly) measure the two variables.
Instead, the product of the variances in the measurements is always greater than some critical value, which
depends on the extent to which the two operators do not commute.
For instance, displacement and momentum are represented (in real-space) by the
operators  and
and
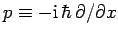 , respectively.
Now, it is easily demonstrated that
, respectively.
Now, it is easily demonstrated that
![\begin{displaymath}[x,p]= {\rm i} \hbar.
\end{displaymath}](img624.png) |
(234) |
Thus,
 |
(235) |
which can be recognized as the standard displacement-momentum uncertainty
principle (see Sect. 3.14). It turns out that the minimum uncertainty (i.e.,
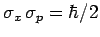 ) is only achieved by Gaussian wave packets (see Sect. 3.12): i.e.,
) is only achieved by Gaussian wave packets (see Sect. 3.12): i.e.,
where 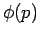 is the momentum-space equivalent of
is the momentum-space equivalent of 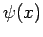 .
.
Energy and time are represented by the operators
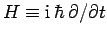 and
and  , respectively. These operators do not commute,
indicating that energy and time cannot be measured simultaneously.
In fact,
, respectively. These operators do not commute,
indicating that energy and time cannot be measured simultaneously.
In fact,
![\begin{displaymath}[H,t]= {\rm i} \hbar,
\end{displaymath}](img633.png) |
(238) |
so
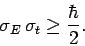 |
(239) |
This can be written, somewhat less exactly, as
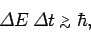 |
(240) |
where 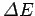 and
and
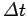 are the uncertainties in
energy and time, respectively. The above expression is generally
known as the energy-time uncertainty principle.
are the uncertainties in
energy and time, respectively. The above expression is generally
known as the energy-time uncertainty principle.
For instance, suppose that a particle passes some fixed point on the  -axis.
Since the particle is, in reality, an extended wave packet, it takes a certain amount
of time
-axis.
Since the particle is, in reality, an extended wave packet, it takes a certain amount
of time 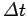 for the particle to pass. Thus, there is an uncertainty,
for the particle to pass. Thus, there is an uncertainty,
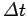 , in the arrival time of the particle. Moreover, since
, in the arrival time of the particle. Moreover, since
 , the only wavefunctions which have unique energies
are those with unique frequencies: i.e., plane waves. Since a
wave packet of finite extent is made up of a combination of plane waves
of different wavenumbers, and, hence, different frequencies, there will
be an uncertainty
, the only wavefunctions which have unique energies
are those with unique frequencies: i.e., plane waves. Since a
wave packet of finite extent is made up of a combination of plane waves
of different wavenumbers, and, hence, different frequencies, there will
be an uncertainty 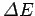 in the particle's energy which is
proportional to the range of frequencies of the plane waves making up the
wave packet. The more compact the wave packet (and, hence, the
smaller
in the particle's energy which is
proportional to the range of frequencies of the plane waves making up the
wave packet. The more compact the wave packet (and, hence, the
smaller 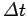 ), the larger the range of frequencies of the constituent plane waves (and, hence, the large
), the larger the range of frequencies of the constituent plane waves (and, hence, the large 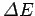 ), and
vice versa. To be more exact, if
), and
vice versa. To be more exact, if  is the wavefunction
measured at the fixed point as a function of time, then we can write
is the wavefunction
measured at the fixed point as a function of time, then we can write
 |
(241) |
In other words, we can express  as a linear combination of
plane waves of definite energy
as a linear combination of
plane waves of definite energy 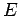 . Here,
. Here, 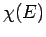 is the complex
amplitude of plane waves of energy
is the complex
amplitude of plane waves of energy 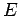 in this combination. By Fourier's
theorem, we also have
in this combination. By Fourier's
theorem, we also have
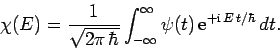 |
(242) |
For instance, if  is a Gaussian then it is easily shown that
is a Gaussian then it is easily shown that
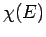 is also a Gaussian: i.e.,
is also a Gaussian: i.e.,
where
 . As before, Gaussian wave packets
satisfy the minimum uncertainty principle
. As before, Gaussian wave packets
satisfy the minimum uncertainty principle
 . Conversely, non-Gaussian wave packets
are characterized by
. Conversely, non-Gaussian wave packets
are characterized by
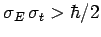 .
.



Next: Eigenstates and Eigenvalues
Up: Fundamentals of Quantum Mechanics
Previous: Momentum Representation
Richard Fitzpatrick
2010-07-20
![]() , where
, where ![]() is an Hermitian operator,
and
is an Hermitian operator,
and ![]() a general wavefunction. We have
a general wavefunction. We have

![]() and
and ![]() ,
and these operators do not commute (i.e.,
,
and these operators do not commute (i.e., ![]() ),
then it is impossible to simultaneously (exactly) measure the two variables.
Instead, the product of the variances in the measurements is always greater than some critical value, which
depends on the extent to which the two operators do not commute.
),
then it is impossible to simultaneously (exactly) measure the two variables.
Instead, the product of the variances in the measurements is always greater than some critical value, which
depends on the extent to which the two operators do not commute.
![]() and
and
![]() , respectively.
Now, it is easily demonstrated that
, respectively.
Now, it is easily demonstrated that
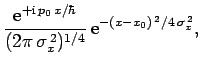
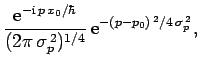
![]() and
and ![]() , respectively. These operators do not commute,
indicating that energy and time cannot be measured simultaneously.
In fact,
, respectively. These operators do not commute,
indicating that energy and time cannot be measured simultaneously.
In fact,
![]() -axis.
Since the particle is, in reality, an extended wave packet, it takes a certain amount
of time
-axis.
Since the particle is, in reality, an extended wave packet, it takes a certain amount
of time ![]() for the particle to pass. Thus, there is an uncertainty,
for the particle to pass. Thus, there is an uncertainty,
![]() , in the arrival time of the particle. Moreover, since
, in the arrival time of the particle. Moreover, since
![]() , the only wavefunctions which have unique energies
are those with unique frequencies: i.e., plane waves. Since a
wave packet of finite extent is made up of a combination of plane waves
of different wavenumbers, and, hence, different frequencies, there will
be an uncertainty
, the only wavefunctions which have unique energies
are those with unique frequencies: i.e., plane waves. Since a
wave packet of finite extent is made up of a combination of plane waves
of different wavenumbers, and, hence, different frequencies, there will
be an uncertainty ![]() in the particle's energy which is
proportional to the range of frequencies of the plane waves making up the
wave packet. The more compact the wave packet (and, hence, the
smaller
in the particle's energy which is
proportional to the range of frequencies of the plane waves making up the
wave packet. The more compact the wave packet (and, hence, the
smaller ![]() ), the larger the range of frequencies of the constituent plane waves (and, hence, the large
), the larger the range of frequencies of the constituent plane waves (and, hence, the large ![]() ), and
vice versa. To be more exact, if
), and
vice versa. To be more exact, if ![]() is the wavefunction
measured at the fixed point as a function of time, then we can write
is the wavefunction
measured at the fixed point as a function of time, then we can write