


Next: Measurement
Up: Fundamentals of Quantum Mechanics
Previous: Heisenberg's Uncertainty Principle
Eigenstates and Eigenvalues
Consider a general real-space operator 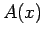 . When this operator
acts on a general wavefunction
. When this operator
acts on a general wavefunction 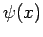 the result is usually a wavefunction
with a completely different shape. However, there are certain special
wavefunctions which are such that when
the result is usually a wavefunction
with a completely different shape. However, there are certain special
wavefunctions which are such that when  acts on them the
result is just a multiple of the original wavefunction. These special
wavefunctions are called eigenstates, and the multiples
are called eigenvalues. Thus, if
acts on them the
result is just a multiple of the original wavefunction. These special
wavefunctions are called eigenstates, and the multiples
are called eigenvalues. Thus, if
 |
(245) |
where 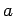 is a complex number, then
is a complex number, then 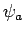 is called an eigenstate of
is called an eigenstate of
 corresponding to the eigenvalue
corresponding to the eigenvalue 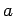 .
.
Suppose that  is an Hermitian operator corresponding to some physical dynamical
variable.
Consider a particle whose wavefunction is
is an Hermitian operator corresponding to some physical dynamical
variable.
Consider a particle whose wavefunction is 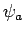 . The expectation of
value
. The expectation of
value  in this state is simply [see Eq. (192)]
in this state is simply [see Eq. (192)]
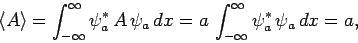 |
(246) |
where use has been made of Eq. (245) and the normalization
condition (140). Moreover,
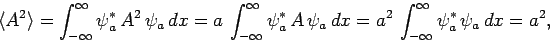 |
(247) |
so
the variance of  is [cf., Eq. (160)]
is [cf., Eq. (160)]
 |
(248) |
The fact that the variance is zero implies that every measurement of  is bound to
yield the same result: namely,
is bound to
yield the same result: namely, 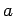 . Thus, the eigenstate
. Thus, the eigenstate 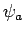 is a state which is
associated with a unique value of the dynamical variable corresponding to
is a state which is
associated with a unique value of the dynamical variable corresponding to  . This
unique value is simply the associated eigenvalue.
. This
unique value is simply the associated eigenvalue.
It is easily demonstrated that the eigenvalues of an Hermitian operator
are all real. Recall [from Eq. (222)] that an
Hermitian operator satisfies
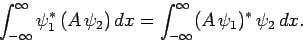 |
(249) |
Hence, if
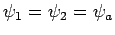 then
then
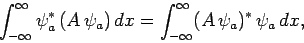 |
(250) |
which reduces to [see Eq. (245)]
 |
(251) |
assuming that  is properly normalized.
is properly normalized.
Two wavefunctions,  and
and  , are said to be orthogonal
if
, are said to be orthogonal
if
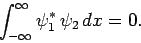 |
(252) |
Consider two eigenstates of  ,
, 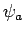 and
and 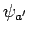 , which
correspond to the two different eigenvalues
, which
correspond to the two different eigenvalues 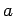 and
and 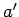 , respectively. Thus,
, respectively. Thus,
Multiplying the complex conjugate of the first equation by 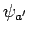 ,
and the second equation by
,
and the second equation by 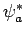 , and then integrating over all
, and then integrating over all
 , we obtain
, we obtain
However, from Eq. (249), the left-hand sides of the above two
equations are equal. Hence, we can
write
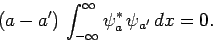 |
(257) |
By assumption, 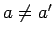 , yielding
, yielding
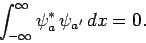 |
(258) |
In other words, eigenstates of an Hermitian operator corresponding to
different eigenvalues are automatically orthogonal.
Consider two eigenstates of  ,
, 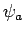 and
and  , which
correspond to the same eigenvalue,
, which
correspond to the same eigenvalue, 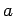 . Such eigenstates
are termed degenerate. The above proof of the orthogonality
of different eigenstates fails for degenerate eigenstates.
Note, however, that any linear combination of
. Such eigenstates
are termed degenerate. The above proof of the orthogonality
of different eigenstates fails for degenerate eigenstates.
Note, however, that any linear combination of
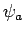 and
and  is also an eigenstate of
is also an eigenstate of  corresponding
to the eigenvalue
corresponding
to the eigenvalue 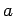 . Thus, even if
. Thus, even if 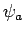 and
and  are not
orthogonal, we can always choose two linear combinations
of these eigenstates which are orthogonal. For instance,
if
are not
orthogonal, we can always choose two linear combinations
of these eigenstates which are orthogonal. For instance,
if 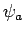 and
and  are properly normalized, and
are properly normalized, and
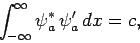 |
(259) |
then it is easily demonstrated that
 |
(260) |
is a properly normalized eigenstate of  , corresponding to the
eigenvalue
, corresponding to the
eigenvalue 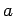 , which is orthogonal to
, which is orthogonal to 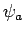 . It is straightforward
to generalize the above argument to three or more degenerate eigenstates.
Hence, we conclude that the eigenstates of an Hermitian
operator are, or can be chosen to be, mutually orthogonal.
. It is straightforward
to generalize the above argument to three or more degenerate eigenstates.
Hence, we conclude that the eigenstates of an Hermitian
operator are, or can be chosen to be, mutually orthogonal.
It is also possible to demonstrate that the eigenstates of an
Hermitian operator form a complete set: i.e., that any
general wavefunction can be written as a linear combination
of these eigenstates. However, the proof is quite difficult, and
we shall not attempt it here.
In summary, given an Hermitian
operator  , any general wavefunction,
, any general wavefunction, 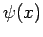 , can be written
, can be written
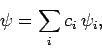 |
(261) |
where the 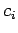 are complex weights, and the
are complex weights, and the 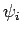 are the properly
normalized (and mutually orthogonal) eigenstates of
are the properly
normalized (and mutually orthogonal) eigenstates of  : i.e.,
: i.e.,
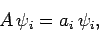 |
(262) |
where 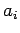 is the eigenvalue corresponding to the eigenstate
is the eigenvalue corresponding to the eigenstate 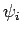 ,
and
,
and
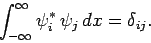 |
(263) |
Here,  is called the Kronecker delta-function, and
takes the value unity when its two indices are equal, and zero otherwise.
is called the Kronecker delta-function, and
takes the value unity when its two indices are equal, and zero otherwise.
It follows from Eqs. (261) and (263)
that
 |
(264) |
Thus, the expansion coefficients in Eq. (261) are easily determined,
given the wavefunction  and the eigenstates
and the eigenstates 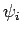 .
Moreover, if
.
Moreover, if  is a properly normalized wavefunction then Eqs. (261) and (263)
yield
is a properly normalized wavefunction then Eqs. (261) and (263)
yield
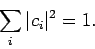 |
(265) |



Next: Measurement
Up: Fundamentals of Quantum Mechanics
Previous: Heisenberg's Uncertainty Principle
Richard Fitzpatrick
2010-07-20
![]() is an Hermitian operator corresponding to some physical dynamical
variable.
Consider a particle whose wavefunction is
is an Hermitian operator corresponding to some physical dynamical
variable.
Consider a particle whose wavefunction is ![]() . The expectation of
value
. The expectation of
value ![]() in this state is simply [see Eq. (192)]
in this state is simply [see Eq. (192)]
![]() and
and ![]() , are said to be orthogonal
if
, are said to be orthogonal
if

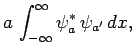


![]() ,
, ![]() and
and ![]() , which
correspond to the same eigenvalue,
, which
correspond to the same eigenvalue, ![]() . Such eigenstates
are termed degenerate. The above proof of the orthogonality
of different eigenstates fails for degenerate eigenstates.
Note, however, that any linear combination of
. Such eigenstates
are termed degenerate. The above proof of the orthogonality
of different eigenstates fails for degenerate eigenstates.
Note, however, that any linear combination of
![]() and
and ![]() is also an eigenstate of
is also an eigenstate of ![]() corresponding
to the eigenvalue
corresponding
to the eigenvalue ![]() . Thus, even if
. Thus, even if ![]() and
and ![]() are not
orthogonal, we can always choose two linear combinations
of these eigenstates which are orthogonal. For instance,
if
are not
orthogonal, we can always choose two linear combinations
of these eigenstates which are orthogonal. For instance,
if ![]() and
and ![]() are properly normalized, and
are properly normalized, and

![]() , any general wavefunction,
, any general wavefunction, ![]() , can be written
, can be written