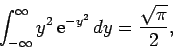Next: Ehrenfest's Theorem
Up: Fundamentals of Quantum Mechanics
Previous: Normalization of the Wavefunction
We have seen that
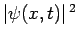 is the probability density of a
measurement of a particle's displacement yielding the value
is the probability density of a
measurement of a particle's displacement yielding the value  at time
at time  .
Suppose that we made a large number of independent measurements of the
displacement on
an equally large number of identical quantum systems. In general, measurements
made on different systems will yield different results. However, from the
definition of probability, the
mean of all these results is simply
.
Suppose that we made a large number of independent measurements of the
displacement on
an equally large number of identical quantum systems. In general, measurements
made on different systems will yield different results. However, from the
definition of probability, the
mean of all these results is simply
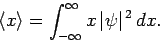 |
(158) |
Here,
 is called the expectation value of
is called the expectation value of  .
Similarly the expectation value of any function of
.
Similarly the expectation value of any function of  is
is
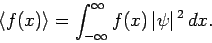 |
(159) |
In general, the results of the various different measurements of  will be scattered
around the expectation value
will be scattered
around the expectation value
 . The
degree of scatter is parameterized by the quantity
. The
degree of scatter is parameterized by the quantity
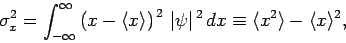 |
(160) |
which is known as the variance of  . The square-root of this
quantity,
. The square-root of this
quantity, 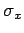 , is called the standard deviation of
, is called the standard deviation of  .
We generally expect the results of measurements of
.
We generally expect the results of measurements of  to lie
within a few standard deviations of the expectation value.
to lie
within a few standard deviations of the expectation value.
For instance, consider the normalized Gaussian wave packet [see Eq. (146)]
 |
(161) |
The expectation value of  associated with this wavefunction is
associated with this wavefunction is
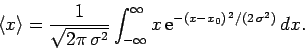 |
(162) |
Let
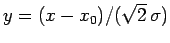 . It follows that
. It follows that
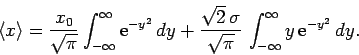 |
(163) |
However, the second integral on the right-hand side is zero, by symmetry.
Hence, making use of Eq. (144), we obtain
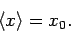 |
(164) |
Evidently, the expectation value of  for a Gaussian wave packet is
equal to the most likely value of
for a Gaussian wave packet is
equal to the most likely value of  (i.e., the value of
(i.e., the value of  which
maximizes
which
maximizes 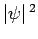 ).
).
The variance of  associated with the Gaussian wave packet (161)
is
associated with the Gaussian wave packet (161)
is
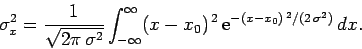 |
(165) |
Let
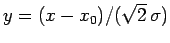 . It follows that
. It follows that
 |
(166) |
However,
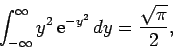 |
(167) |
giving
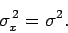 |
(168) |
This result is consistent with our earlier interpretation of  as a measure of the
spatial extent of the wave packet (see Sect. 3.12).
It follows that we can rewrite the Gaussian wave packet (161) in the convenient form
as a measure of the
spatial extent of the wave packet (see Sect. 3.12).
It follows that we can rewrite the Gaussian wave packet (161) in the convenient form
 |
(169) |



Next: Ehrenfest's Theorem
Up: Fundamentals of Quantum Mechanics
Previous: Normalization of the Wavefunction
Richard Fitzpatrick
2010-07-20
![]() will be scattered
around the expectation value
will be scattered
around the expectation value
![]() . The
degree of scatter is parameterized by the quantity
. The
degree of scatter is parameterized by the quantity
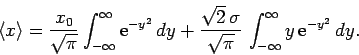
![]() associated with the Gaussian wave packet (161)
is
associated with the Gaussian wave packet (161)
is