


Next: Momentum Representation
Up: Fundamentals of Quantum Mechanics
Previous: Ehrenfest's Theorem
Operators
An operator, 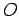 (say), is a mathematical entity which transforms
one function into another: i.e.,
(say), is a mathematical entity which transforms
one function into another: i.e.,
 |
(184) |
For instance,  is an operator, since
is an operator, since  is a different function
to
is a different function
to 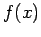 , and is fully specified once
, and is fully specified once 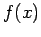 is given. Furthermore,
is given. Furthermore,
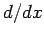 is also an operator, since
is also an operator, since 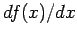 is a different function
to
is a different function
to 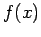 , and is fully specified once
, and is fully specified once 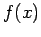 is given.
Now,
is given.
Now,
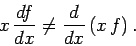 |
(185) |
This can also be written
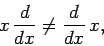 |
(186) |
where the operators are assumed to act on everything to
their right, and a final 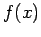 is understood [where
is understood [where 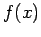 is a general function]. The above expression illustrates
an important point: i.e., in general, operators do not
commute. Of course, some operators do commute: e.g.,
is a general function]. The above expression illustrates
an important point: i.e., in general, operators do not
commute. Of course, some operators do commute: e.g.,
 |
(187) |
Finally, an operator, 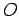 , is termed linear if
, is termed linear if
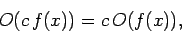 |
(188) |
where  is a general function, and
is a general function, and 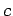 a general complex number.
All of the operators employed in quantum mechanics are linear.
a general complex number.
All of the operators employed in quantum mechanics are linear.
Now, from Eqs. (158) and (174),
These expressions suggest a number of things. First, classical dynamical
variables, such as  and
and 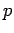 , are represented in quantum mechanics
by linear operators which act on the wavefunction. Second,
displacement is represented by the algebraic operator
, are represented in quantum mechanics
by linear operators which act on the wavefunction. Second,
displacement is represented by the algebraic operator  ,
and momentum by the differential operator
,
and momentum by the differential operator
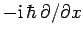 : i.e.,
: i.e.,
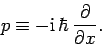 |
(191) |
Finally, the expectation value of some dynamical variable represented by
the operator 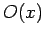 is simply
is simply
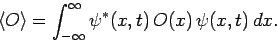 |
(192) |
Clearly, if an operator is to represent a dynamical variable which has
physical significance then its expectation value must be real.
In other words, if the operator 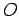 represents a physical variable
then we require that
represents a physical variable
then we require that
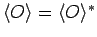 , or
, or
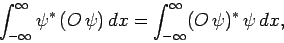 |
(193) |
where 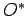 is the complex conjugate of
is the complex conjugate of 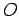 . An operator which
satisfies the above constraint is called an Hermitian operator.
It is easily demonstrated that
. An operator which
satisfies the above constraint is called an Hermitian operator.
It is easily demonstrated that  and
and 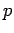 are both Hermitian.
The Hermitian conjugate,
are both Hermitian.
The Hermitian conjugate, 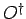 , of
a general operator,
, of
a general operator, 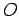 , is defined as follows:
, is defined as follows:
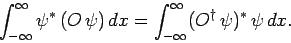 |
(194) |
The Hermitian conjugate of an Hermitian operator is the same as the operator
itself: i.e., 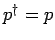 . For a non-Hermitian operator,
. For a non-Hermitian operator, 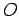 (say),
it is easily demonstrated that
(say),
it is easily demonstrated that
 , and that the operator
, and that the operator 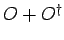 is Hermitian.
Finally, if
is Hermitian.
Finally, if  and
and  are two operators, then
are two operators, then
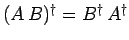 .
.
Suppose that we wish to find the operator which corresponds to the
classical dynamical variable 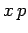 . In classical mechanics, there
is no difference between
. In classical mechanics, there
is no difference between 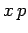 and
and 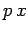 . However, in quantum
mechanics, we have already seen that
. However, in quantum
mechanics, we have already seen that 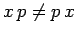 . So,
should be choose
. So,
should be choose 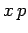 or
or 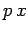 ? Actually, neither of these combinations
is Hermitian. However,
? Actually, neither of these combinations
is Hermitian. However,
![$(1/2) [x p + (x p)^\dag ]$](img554.png) is Hermitian.
Moreover,
is Hermitian.
Moreover,
![$(1/2) [x p + (x p)^\dag ]=(1/2) (x p+p^\dag x^\dag )=(1/2) (x p+p x)$](img555.png) , which neatly resolves
our problem of which order to put
, which neatly resolves
our problem of which order to put  and
and 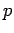 .
.
It is a reasonable guess that the operator corresponding to energy (which is
called the Hamiltonian, and conventionally denoted 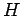 ) takes the form
) takes the form
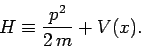 |
(195) |
Note that 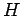 is Hermitian. Now, it follows from Eq. (191) that
is Hermitian. Now, it follows from Eq. (191) that
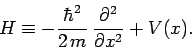 |
(196) |
However, according to Schrödinger's equation, (137), we have
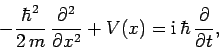 |
(197) |
so
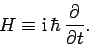 |
(198) |
Thus, the time-dependent Schrödinger equation can be written
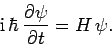 |
(199) |
Finally, if 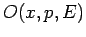 is a classical dynamical variable which is
a function of displacement, momentum, and energy, then a reasonable
guess for the corresponding operator in quantum mechanics is
is a classical dynamical variable which is
a function of displacement, momentum, and energy, then a reasonable
guess for the corresponding operator in quantum mechanics is
![$(1/2) [O(x,p,H)+ O^\dag (x,p,H)]$](img563.png) , where
, where
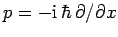 , and
, and
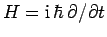 .
.



Next: Momentum Representation
Up: Fundamentals of Quantum Mechanics
Previous: Ehrenfest's Theorem
Richard Fitzpatrick
2010-07-20

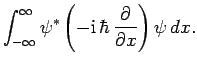
![]() represents a physical variable
then we require that
represents a physical variable
then we require that
![]() , or
, or
![]() . In classical mechanics, there
is no difference between
. In classical mechanics, there
is no difference between ![]() and
and ![]() . However, in quantum
mechanics, we have already seen that
. However, in quantum
mechanics, we have already seen that ![]() . So,
should be choose
. So,
should be choose ![]() or
or ![]() ? Actually, neither of these combinations
is Hermitian. However,
? Actually, neither of these combinations
is Hermitian. However,
![]() is Hermitian.
Moreover,
is Hermitian.
Moreover,
![]() , which neatly resolves
our problem of which order to put
, which neatly resolves
our problem of which order to put ![]() and
and ![]() .
.
![]() ) takes the form
) takes the form
![]() is a classical dynamical variable which is
a function of displacement, momentum, and energy, then a reasonable
guess for the corresponding operator in quantum mechanics is
is a classical dynamical variable which is
a function of displacement, momentum, and energy, then a reasonable
guess for the corresponding operator in quantum mechanics is
![]() , where
, where
![]() , and
, and
![]() .
.