


Next: Normalization of the Wavefunction
Up: Fundamentals of Quantum Mechanics
Previous: Introduction
Consider a dynamical system consisting of a single non-relativistic particle of mass 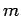 moving along the
moving along the  -axis in some real potential
-axis in some real potential 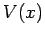 . In quantum mechanics, the instantaneous state of the system is represented by a complex wavefunction
. In quantum mechanics, the instantaneous state of the system is represented by a complex wavefunction 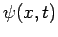 . This wavefunction evolves in time
according to Schrödinger's equation:
. This wavefunction evolves in time
according to Schrödinger's equation:
 |
(137) |
The wavefunction is interpreted as follows:
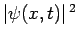 is
the probability density of a measurement of the particle's
displacement yielding the value
is
the probability density of a measurement of the particle's
displacement yielding the value  . Thus, the probability of
a measurement of the displacement giving a result
between
. Thus, the probability of
a measurement of the displacement giving a result
between 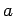 and
and 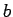 (where
(where 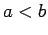 ) is
) is
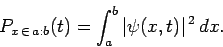 |
(138) |
Note that this quantity is real and positive definite.
Richard Fitzpatrick
2010-07-20