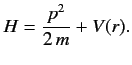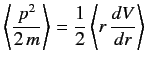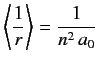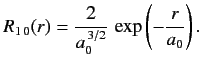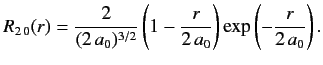Next: Spin Angular Momentum
Up: Orbital Angular Momentum
Previous: Energy Levels of Hydrogen
- Demonstrate directly from the fundamental commutation relations for angular momentum, (300), that
![$ [L^2, L_z] = 0$](img990.png) ,
,
![$ [L^\pm, L_z] = \mp \,\hbar\,L^\pm$](img991.png) , and
, and
![$ [L^+,L^-] = 2\,\hbar\,L_z$](img992.png) .
.
- Demonstrate from Equations (363)-(368) that
where  ,
, 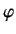 are conventional spherical polar angles.
are conventional spherical polar angles.
- A system is in the state
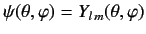 . Evaluate
. Evaluate
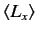 ,
,
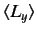 ,
,
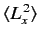 , and
, and
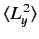 .
.
- Derive Equations (385) and (386) from Equation (384).
- Find the eigenvalues and eigenfunctions (in terms of the angles
 and
and 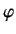 ) of
) of 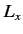 .
.
- Consider a beam of particles with
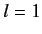 . A measurement of
. A measurement of 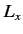 yields the result
yields the result 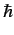 . What
values will be obtained by a subsequent measurement of
. What
values will be obtained by a subsequent measurement of 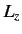 , and with what probabilities? Repeat
the calculation for the cases in which the measurement of
, and with what probabilities? Repeat
the calculation for the cases in which the measurement of 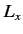 yields the results 0
and
yields the results 0
and
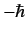 .
.
- The Hamiltonian for an axially symmetric rotator is given by
What are the eigenvalues of 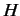 ?
?
- The expectation value of
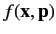 in any stationary state is a constant.
Calculate
in any stationary state is a constant.
Calculate
for a Hamiltonian of the form
Hence, show that
in a stationary state. This is another form of the Virial theorem. (See Exercise 8.)
- Use the Virial theorem of the previous exercise to prove that
for an energy eigenstate of the hydrogen atom.
- Demonstrate that the first few properly normalized radial wavefunctions of the hydrogen atom take the form:



Next: Spin Angular Momentum
Up: Orbital Angular Momentum
Previous: Energy Levels of Hydrogen
Richard Fitzpatrick
2013-04-08
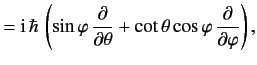
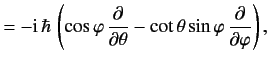
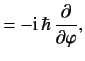

![$\displaystyle 0= \frac{d}{dt}\,(\langle{\bf x}\cdot{\bf p}\rangle) = \frac{{\rm i}}{\hbar}\,\langle[H, {\bf x}\cdot{\bf p}]\rangle
$](img1002.png)
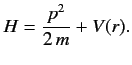
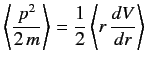
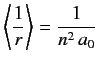
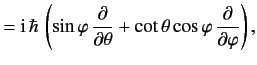
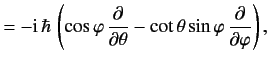
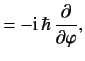

![$\displaystyle 0= \frac{d}{dt}\,(\langle{\bf x}\cdot{\bf p}\rangle) = \frac{{\rm i}}{\hbar}\,\langle[H, {\bf x}\cdot{\bf p}]\rangle
$](img1002.png)