


Next: Exercises
Up: Orbital Angular Momentum
Previous: Motion in Central Field
Energy Levels of Hydrogen Atom
Consider a hydrogen atom, for which the potential takes the specific form
 |
(396) |
The radial eigenfunction 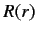 satisfies Equation (395), which can be written
satisfies Equation (395), which can be written
![$\displaystyle \left[\frac{\hbar^2}{2\,\mu} \left(-\frac{1}{r^2} \frac{d}{dr}\,r...
... +\frac{l\,(l+1)}{r^2}\right) -\frac{e^2}{4\pi\,\epsilon_0\,r}- E\right] R = 0.$](img939.png) |
(397) |
Here,
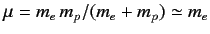 is the reduced mass, which takes into
account the fact that the electron (of mass
is the reduced mass, which takes into
account the fact that the electron (of mass 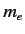 ) and the proton (of mass
) and the proton (of mass 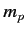 )
both rotate about a common centre, which is equivalent to a particle of
mass
)
both rotate about a common centre, which is equivalent to a particle of
mass 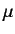 rotating about a fixed point. Let us write the product
rotating about a fixed point. Let us write the product  as the function
as the function 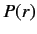 . The above equation transforms to
. The above equation transforms to
![$\displaystyle \frac{d^2 P}{d r^2} - \frac{2\,\mu}{\hbar^2}\left[ \frac{l\,(l+1)\,\hbar^2}{2\,\mu \,r^2} - \frac{e^2}{4\pi \,\epsilon_0 \,r}-E\right] P =0,$](img945.png) |
(398) |
which is the one-dimensional Schrödinger equation for a particle of
mass 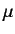 moving in the effective potential
moving in the effective potential
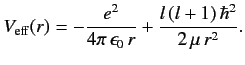 |
(399) |
The effective potential has a simple physical interpretation. The first part is the
attractive Coulomb potential, and the second part corresponds
to the repulsive centrifugal force.
Let
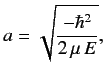 |
(400) |
and 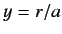 , with
, with
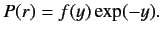 |
(401) |
Here, it is assumed that the energy eigenvalue 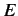 is negative.
Equation (398) transforms to
is negative.
Equation (398) transforms to
 |
(402) |
Let us look for a power-law solution of the form
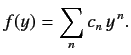 |
(403) |
Substituting this solution into Equation (402), we obtain
![$\displaystyle \sum_n c_n \left[ n\,(n-1)\,y^{\,n-2} - 2\,n\, y^{\,n-1} - l\,(l+...
...+ \frac{2\,\mu\, e^2 \,a}{4\pi\, \epsilon_0 \,\hbar^2}\, y^{\,n-1} \right] = 0.$](img952.png) |
(404) |
Equating the coefficients of 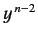 gives
gives
![$\displaystyle c_n\,[n\,(n-1) - l\,(l+1)] = c_{n-1} \left [2\,(n-1) - \frac{2\,\mu\, e^2\, a}{4\pi\, \epsilon_0\, \hbar^2}\right].$](img954.png) |
(405) |
Now, the power law series (403) must terminate at small 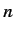 , at some positive
value of
, at some positive
value of 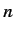 , otherwise
, otherwise 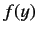 would behave unphysically as
would behave unphysically as
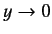 . This
is only possible if
. This
is only possible if
![$ [n_{\rm min} (n_{\rm min} -1) - l\,(l+1) ] =0$](img957.png) , where
the first term in the series is
, where
the first term in the series is
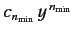 . There
are two possibilities:
. There
are two possibilities:
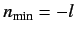 or
or
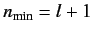 . The
former predicts unphysical behavior of the wavefunction at
. The
former predicts unphysical behavior of the wavefunction at 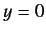 .
Thus, we conclude that
.
Thus, we conclude that
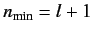 . Note that for an
. Note that for an 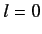 state
there is a finite probability of finding the electron at the nucleus,
whereas for an
state
there is a finite probability of finding the electron at the nucleus,
whereas for an 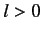 state there is zero probability of finding
the electron at the nucleus (i.e.,
state there is zero probability of finding
the electron at the nucleus (i.e.,
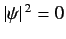 at
at 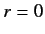 , except when
, except when
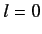 ). Note, also, that it is only possible to obtain sensible behavior of the
wavefunction as
). Note, also, that it is only possible to obtain sensible behavior of the
wavefunction as
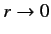 if
if  is an integer.
is an integer.
For large values of 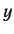 , the ratio of successive terms in the series
(403) is
, the ratio of successive terms in the series
(403) is
 |
(406) |
according to Equation (405). This is the same as the ratio of
successive terms in the series
 |
(407) |
which converges to
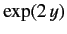 . We conclude that
. We conclude that
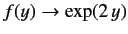 as
as
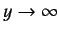 . It follows from Equation (401) that
. It follows from Equation (401) that
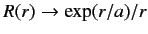 as
as
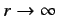 . This does not correspond to
physically acceptable behavior of the wavefunction, since
. This does not correspond to
physically acceptable behavior of the wavefunction, since
 must be finite. The only way in which we can avoid this unphysical
behavior is if the series (403) terminates at some maximum value of
must be finite. The only way in which we can avoid this unphysical
behavior is if the series (403) terminates at some maximum value of 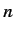 .
According to the recursion relation (405), this is only possible
if
.
According to the recursion relation (405), this is only possible
if
 |
(408) |
where the last term in the series is
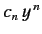 . It follows from Equation (400)
that the energy eigenvalues are quantized, and can only take the values
. It follows from Equation (400)
that the energy eigenvalues are quantized, and can only take the values
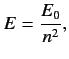 |
(409) |
where
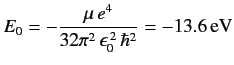 |
(410) |
is the ground state energy.
Here, 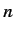 is a positive integer which must exceed the quantum number
is a positive integer which must exceed the quantum number  ,
otherwise there would be no terms in the series (403).
,
otherwise there would be no terms in the series (403).
The properly normalized wavefunction of a hydrogen atom is written
 |
(411) |
where
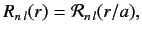 |
(412) |
and
 |
(413) |
Here,
 |
(414) |
is the Bohr radius, and
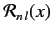 is a well-behaved solution of the differential equation
is a well-behaved solution of the differential equation
![$\displaystyle \left[\frac{1}{x^2} \frac{d}{dx}\, x^2 \,\frac{d}{dx}-\frac{l\,(l+1)}{x^2} + \frac{2\,n}{x} - 1\right] {\cal R}_{n\,l} = 0$](img981.png) |
(415) |
that is consistent with the normalization constraint
![$\displaystyle \int_0^\infty dr\,r^2\,[R_{n\,l}(r)]^{\,2}= 1.$](img982.png) |
(416) |
Finally, the  are spherical harmonics. The restrictions on the quantum numbers
are
are spherical harmonics. The restrictions on the quantum numbers
are
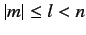 , where
, where 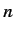 is a positive integer,
is a positive integer,  a non-negative integer, and
a non-negative integer, and  an integer.
an integer.
The ground state of hydrogen corresponds to 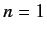 . The only permissible values
of the other quantum numbers are
. The only permissible values
of the other quantum numbers are 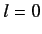 and
and 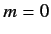 . Thus, the ground state is
a spherically symmetric, zero angular momentum state. The next energy level corresponds to
. Thus, the ground state is
a spherically symmetric, zero angular momentum state. The next energy level corresponds to 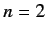 . The other quantum numbers are
allowed to take the values
. The other quantum numbers are
allowed to take the values 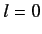 ,
, 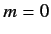 or
or 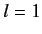 ,
,
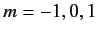 . Thus, there are
. Thus, there are
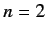 states with non-zero angular momentum. Note that the energy levels given
in Equation (409) are independent of the quantum number
states with non-zero angular momentum. Note that the energy levels given
in Equation (409) are independent of the quantum number  , despite the fact that
, despite the fact that
 appears in the radial eigenfunction equation (415). This is a special
property of a
appears in the radial eigenfunction equation (415). This is a special
property of a  Coulomb potential.
Coulomb potential.
In addition to the quantized negative energy states of the
hydrogen atom, which we have just found, there
is also a continuum of unbound positive energy states.



Next: Exercises
Up: Orbital Angular Momentum
Previous: Motion in Central Field
Richard Fitzpatrick
2013-04-08


![$\displaystyle \left[\frac{\hbar^2}{2\,\mu} \left(-\frac{1}{r^2} \frac{d}{dr}\,r...
... +\frac{l\,(l+1)}{r^2}\right) -\frac{e^2}{4\pi\,\epsilon_0\,r}- E\right] R = 0.$](img939.png)
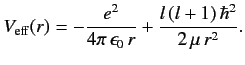
![$\displaystyle \sum_n c_n \left[ n\,(n-1)\,y^{\,n-2} - 2\,n\, y^{\,n-1} - l\,(l+...
...+ \frac{2\,\mu\, e^2 \,a}{4\pi\, \epsilon_0 \,\hbar^2}\, y^{\,n-1} \right] = 0.$](img952.png)
![]() , the ratio of successive terms in the series
(403) is
, the ratio of successive terms in the series
(403) is



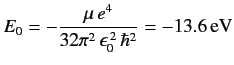

![$\displaystyle \int_0^\infty dr\,r^2\,[R_{n\,l}(r)]^{\,2}= 1.$](img982.png)
![]() . The only permissible values
of the other quantum numbers are
. The only permissible values
of the other quantum numbers are ![]() and
and ![]() . Thus, the ground state is
a spherically symmetric, zero angular momentum state. The next energy level corresponds to
. Thus, the ground state is
a spherically symmetric, zero angular momentum state. The next energy level corresponds to ![]() . The other quantum numbers are
allowed to take the values
. The other quantum numbers are
allowed to take the values ![]() ,
, ![]() or
or ![]() ,
,
![]() . Thus, there are
. Thus, there are
![]() states with non-zero angular momentum. Note that the energy levels given
in Equation (409) are independent of the quantum number
states with non-zero angular momentum. Note that the energy levels given
in Equation (409) are independent of the quantum number ![]() , despite the fact that
, despite the fact that
![]() appears in the radial eigenfunction equation (415). This is a special
property of a
appears in the radial eigenfunction equation (415). This is a special
property of a ![]() Coulomb potential.
Coulomb potential.