


Next: Eigenvalues of Orbital Angular
Up: Orbital Angular Momentum
Previous: Orbital Angular Momentum
Orbital Angular Momentum
Consider a particle described by the Cartesian coordinates
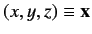 and their conjugate momenta
and their conjugate momenta
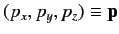 . The classical
definition of the orbital angular momentum of such a particle about the
origin is
. The classical
definition of the orbital angular momentum of such a particle about the
origin is
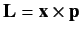 , giving
, giving
Let us assume that the operators
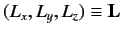 which
represent the components of
orbital angular momentum in quantum mechanics can be defined in
an analogous manner to the corresponding components of
classical angular momentum. In other words, we are
going to assume that the above equations specify the angular momentum operators
in terms of the position and linear momentum operators. Note that
which
represent the components of
orbital angular momentum in quantum mechanics can be defined in
an analogous manner to the corresponding components of
classical angular momentum. In other words, we are
going to assume that the above equations specify the angular momentum operators
in terms of the position and linear momentum operators. Note that 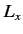 ,
, 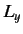 ,
and
,
and 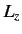 are Hermitian, so they represent things which can, in principle,
be measured. Note, also, that there is no ambiguity regarding the order
in which operators appear in products on the right-hand sides of Equations (290)-(292),
because all of the products consist of operators that commute.
are Hermitian, so they represent things which can, in principle,
be measured. Note, also, that there is no ambiguity regarding the order
in which operators appear in products on the right-hand sides of Equations (290)-(292),
because all of the products consist of operators that commute.
The fundamental commutation relations satisfied by the
position and linear momentum operators are [see Equations (114)-(116)]
where 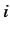 and
and 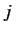 stand for either
stand for either  ,
, 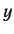 , or
, or  .
Consider the commutator of the operators
.
Consider the commutator of the operators 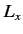 and
and 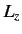 :
:
The cyclic permutations of the above result yield
the fundamental commutation relations satisfied
by the components of an orbital angular momentum:
These can be summed up more succinctly by writing
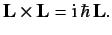 |
(300) |
The three commutation relations (297)-(299) are the foundation for the whole
theory of angular momentum in quantum mechanics. Whenever we encounter
three operators having these commutation relations, we know that the
dynamical variables that they represent have identical properties
to those of the components of an
angular momentum (which we are about to derive). In fact,
we shall assume that any three operators that satisfy the commutation
relations (297)-(299) represent the components of some sort of angular momentum.
Suppose that there are 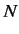 particles in the system, with
angular momentum vectors
particles in the system, with
angular momentum vectors 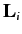 (where
(where 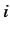 runs from 1 to
runs from 1 to 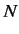 ).
Each of these vectors satisfies Equation (300), so that
).
Each of these vectors satisfies Equation (300), so that
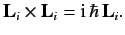 |
(301) |
However, we expect the angular momentum operators
belonging to different particles to commute, because they represent different
degrees of freedom of the system. So,
we can write
 |
(302) |
for 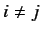 . Consider the total angular momentum of the system,
. Consider the total angular momentum of the system,
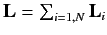 . It is clear from Equations (301) and (302)
that
. It is clear from Equations (301) and (302)
that
Thus, the sum of two or more angular momentum vectors satisfies the
same commutation relation as a primitive angular momentum vector.
In particular, the total angular momentum of the system satisfies the
commutation relation (300).
The immediate conclusion which can be drawn from the commutation relations
(297)-(299) is that the three components of an angular momentum vector cannot
be specified (or measured) simultaneously. In fact, once we have specified one
component, the values of other two components become uncertain. It is
conventional to specify the  -component,
-component, 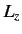 .
.
Consider the magnitude squared of the angular momentum vector,
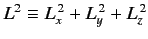 . The commutator of
. The commutator of 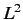 and
and 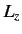 is
written
is
written
![$\displaystyle [L^2, L_z] = [L_x^{\,2}, L_z] + [L_y^{\,2}, L_z] + [L_z^{\,2}, L_z].$](img761.png) |
(304) |
It is easily demonstrated that
so
![$\displaystyle [L^2, L_z] = 0.$](img767.png) |
(308) |
Because there is nothing special about the  -direction, we conclude that
-direction, we conclude that 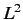 also
commutes with
also
commutes with 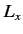 and
and 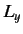 . It is clear from Equations (297)-(299) and
(308) that the best we
can do in quantum mechanics is to specify the
magnitude of an angular momentum vector
along with one of its components (by convention, the
. It is clear from Equations (297)-(299) and
(308) that the best we
can do in quantum mechanics is to specify the
magnitude of an angular momentum vector
along with one of its components (by convention, the  -component).
-component).
It is convenient to define the shift operators 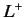 and
and 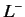 :
:
It can easily be shown that
and also that both shift operators commute with 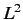 .
.



Next: Eigenvalues of Orbital Angular
Up: Orbital Angular Momentum
Previous: Orbital Angular Momentum
Richard Fitzpatrick
2013-04-08
![]() particles in the system, with
angular momentum vectors
particles in the system, with
angular momentum vectors ![]() (where
(where ![]() runs from 1 to
runs from 1 to ![]() ).
Each of these vectors satisfies Equation (300), so that
).
Each of these vectors satisfies Equation (300), so that
![]() -component,
-component, ![]() .
.
![]() . The commutator of
. The commutator of ![]() and
and ![]() is
written
is
written
![]() and
and ![]() :
: