


Next: Reflection at a dielectric
Up: Electromagnetic radiation
Previous: Propagation in a conductor
We have now investigated electromagnetic wave propagation
through two different media possessing free electrons: plasmas (see Sect. 9.8), and
ohmic conductors (see Sect. 9.10). In the first case, we
obtained the dispersion relation (1155), whereas in the second
we obtained the quite different dispersion relation (1191).
This leads us, quite naturally, to ask what the essential distinction is between
the response of free electrons in a plasma to an electromagnetic
wave, and that of free electrons in an ohmic conductor.
It turns out that the main distinction is the relative strength of electron-ion
collisions.
In the presence of electron-ion collisions, we can model the equation
of motion of an individual electron in a plasma or a conductor as
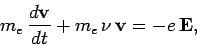 |
(1201) |
where 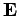 is the wave electric field. The collision term (i.e., the second term on the left-hand side) takes the form of
a drag force proportional to
is the wave electric field. The collision term (i.e., the second term on the left-hand side) takes the form of
a drag force proportional to 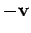 . In the absence of the wave electric
field, this force damps out any electron motion on the typical time-scale
. In the absence of the wave electric
field, this force damps out any electron motion on the typical time-scale
 . Since, in reality, an electron loses virtually all of its directed momentum during a collision with a much more massive ion, we can regard
. Since, in reality, an electron loses virtually all of its directed momentum during a collision with a much more massive ion, we can regard
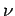 as the effective electron-ion collision frequency.
as the effective electron-ion collision frequency.
Assuming the usual
 time-dependence of
perturbed quantities, we can solve Eq. (1201)
to give
time-dependence of
perturbed quantities, we can solve Eq. (1201)
to give
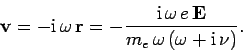 |
(1202) |
Hence, the perturbed current density can be written
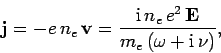 |
(1203) |
where  is the number density of free electrons.
It follows that the effective conductivity of the medium takes the form
is the number density of free electrons.
It follows that the effective conductivity of the medium takes the form
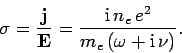 |
(1204) |
Now, the mean rate of ohmic heating per unit volume in the medium is
written
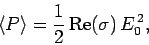 |
(1205) |
where 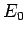 is the amplitude of the wave electric field. Note that
only the real part of
is the amplitude of the wave electric field. Note that
only the real part of 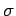 contributes to ohmic heating, because the
perturbed current must be in phase with the wave electric field
in order for there to be a net heating effect. An imaginary
contributes to ohmic heating, because the
perturbed current must be in phase with the wave electric field
in order for there to be a net heating effect. An imaginary 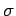 gives a
perturbed current which is in phase quadrature with the wave electric field.
In this case, there is zero net transfer of power between the wave and the plasma over a wave period. We can see from Eq. (1204)
that in the limit in which the wave frequency is much larger than the
collision frequency (i.e.,
gives a
perturbed current which is in phase quadrature with the wave electric field.
In this case, there is zero net transfer of power between the wave and the plasma over a wave period. We can see from Eq. (1204)
that in the limit in which the wave frequency is much larger than the
collision frequency (i.e., 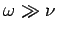 ), the effective
conductivity of the medium becomes purely imaginary:
), the effective
conductivity of the medium becomes purely imaginary:
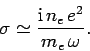 |
(1206) |
In this limit, there is no loss of wave energy due to ohmic heating, and
the medium acts like a conventional plasma. In the opposite limit, in which
the wave frequency is much less than the collision frequency (i.e., 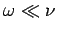 ), the effective conductivity becomes purely real:
), the effective conductivity becomes purely real:
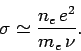 |
(1207) |
In this limit, ohmic heating losses are significant, and the medium acts like
a conventional ohmic conductor.
Following the analysis of Sect. 9.7, we can derive the following
dispersion relation from Eq. (1202):
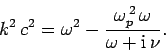 |
(1208) |
It can be seen that, in the limit 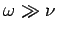 , the above dispersion relation
reduces to the dispersion relation (1155) for a conventional
(i.e., collisionless) plasma. In the opposite limit, we obtain
, the above dispersion relation
reduces to the dispersion relation (1155) for a conventional
(i.e., collisionless) plasma. In the opposite limit, we obtain
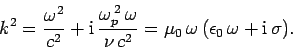 |
(1209) |
where use has been made of Eq (1207). Of course, the
above dispersion relation is identical to the dispersion relation (1191)
(with 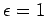 ) which we previously derived for an ohmic
conductor.
) which we previously derived for an ohmic
conductor.
Our main conclusion from this subsection is that the dispersion relation
(1208)
can be used to describe electromagnetic wave propagation through both a collisional plasma and an ohmic
conductor. We can also deduce that in the low frequency limit, 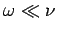 , a collisional
plasma acts very much like an ohmic conductor, whereas in the
high frequency limit,
, a collisional
plasma acts very much like an ohmic conductor, whereas in the
high frequency limit, 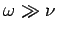 , an ohmic conductor acts very much
like a collisionless plasma.
, an ohmic conductor acts very much
like a collisionless plasma.



Next: Reflection at a dielectric
Up: Electromagnetic radiation
Previous: Propagation in a conductor
Richard Fitzpatrick
2006-02-02
![]() time-dependence of
perturbed quantities, we can solve Eq. (1201)
to give
time-dependence of
perturbed quantities, we can solve Eq. (1201)
to give
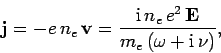
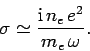
![]() , a collisional
plasma acts very much like an ohmic conductor, whereas in the
high frequency limit,
, a collisional
plasma acts very much like an ohmic conductor, whereas in the
high frequency limit, ![]() , an ohmic conductor acts very much
like a collisionless plasma.
, an ohmic conductor acts very much
like a collisionless plasma.