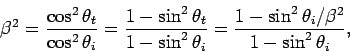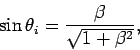Next: Wave-guides
Up: Electromagnetic radiation
Previous: Dielectric constant of a
An electromagnetic wave of real (positive) frequency 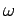 can be written
can be written
The wave-vector, 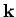 , indicates the direction of propagation of the
wave, and also its phase-velocity,
, indicates the direction of propagation of the
wave, and also its phase-velocity, 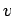 , via
, via
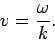 |
(1212) |
Since the wave is transverse in nature, we must have
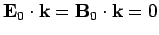 . Finally, the familiar
Maxwell
equation
. Finally, the familiar
Maxwell
equation
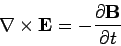 |
(1213) |
leads us to the following relation between the constant vectors 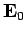 and
and 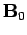 :
:
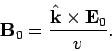 |
(1214) |
Here,
 is a unit vector pointing in the
direction of wave propagation.
is a unit vector pointing in the
direction of wave propagation.
Suppose that the plane 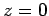 forms the boundary between two different dielectric
media. Let medium 1, of refractive index
forms the boundary between two different dielectric
media. Let medium 1, of refractive index 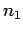 , occupy the region
, occupy the region 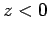 ,
whilst medium 2, of refractive index
,
whilst medium 2, of refractive index 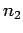 , occupies the region
, occupies the region 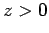 .
Let us investigate what happens when an electromagnetic wave is incident
on this boundary from medium 1.
.
Let us investigate what happens when an electromagnetic wave is incident
on this boundary from medium 1.
Figure 55:
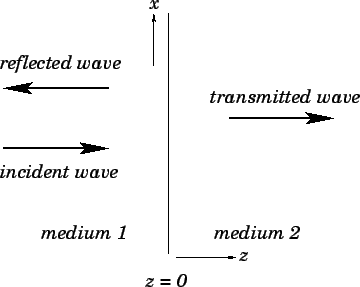 |
Consider, first of all, the simple case of incidence normal
to the boundary (see Fig. 55). In this case,
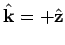 for the
incident and transmitted waves, and
for the
incident and transmitted waves, and
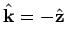 for the reflected wave. Without loss of generality, we can assume that
the incident wave is polarized in the
for the reflected wave. Without loss of generality, we can assume that
the incident wave is polarized in the  -direction.
Hence, using Eq. (1214), the incident
wave can be written
-direction.
Hence, using Eq. (1214), the incident
wave can be written
where 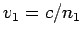 is the phase-velocity in medium 1, and
is the phase-velocity in medium 1, and
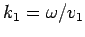 . Likewise, the reflected wave takes the form
. Likewise, the reflected wave takes the form
Finally, the transmitted wave can be written
where 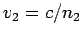 is the phase-velocity in medium 2, and
is the phase-velocity in medium 2, and
 .
.
For the case of normal incidence, the electric and magnetic
components of all three waves are parallel to the boundary between
the two dielectric media. Hence, the appropriate boundary conditions
to apply at  are
are
The latter condition derives from the general boundary condition
 , and the fact that
, and the fact that
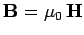 in both media (which are assumed to be non-magnetic).
in both media (which are assumed to be non-magnetic).
Application of the boundary condition
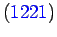 yields
yields
 |
(1223) |
Likewise, application of the boundary condition (1222) gives
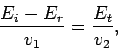 |
(1224) |
or
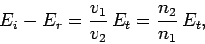 |
(1225) |
since
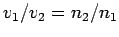 .
Equations (1223) and (1225) can be solved to give
.
Equations (1223) and (1225) can be solved to give
Thus, we have determined the amplitudes of the reflected and transmitted
waves in terms of the amplitude of the incident wave.
It can be seen, first of all, that if 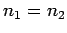 then
then  and
and 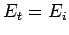 .
In other words, if the two media have the same indices of refraction then
there is no reflection at the boundary between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if
.
In other words, if the two media have the same indices of refraction then
there is no reflection at the boundary between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if  then there is some reflection at the boundary. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between
then there is some reflection at the boundary. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between 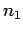 and
and 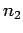 . This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
at an air/glass boundary is reflected, due to the different refractive indicies
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass boundary.
. This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
at an air/glass boundary is reflected, due to the different refractive indicies
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass boundary.
According to Eq. (1226), 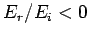 when
when 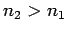 .
The negative sign indicates a
.
The negative sign indicates a 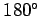 phase-shift of the reflected wave, with
respect to the incident wave. We conclude that there is a
phase-shift of the reflected wave, with
respect to the incident wave. We conclude that there is a 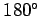 phase-shift of the reflected wave, relative to the incident wave, on reflection from a boundary with a
medium of greater refractive index. Conversely, there is no
phase-shift
on reflection from a boundary with a medium of lesser refractive index.
phase-shift of the reflected wave, relative to the incident wave, on reflection from a boundary with a
medium of greater refractive index. Conversely, there is no
phase-shift
on reflection from a boundary with a medium of lesser refractive index.
The mean electromagnetic energy flux, or intensity, in the  -direction is simply
-direction is simply
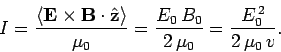 |
(1228) |
The coefficient of reflection,  , is defined as the ratio
of the intensities of the reflected and incident waves:
, is defined as the ratio
of the intensities of the reflected and incident waves:
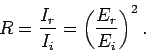 |
(1229) |
Likewise, the coefficient of transmission, 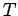 , is the ratio of
the intensities of the transmitted and incident waves:
, is the ratio of
the intensities of the transmitted and incident waves:
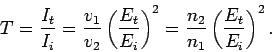 |
(1230) |
Equations (1226), (1227), (1229), and (1230)
yield
Note that 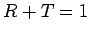 . In other words, any wave energy which is not reflected
at the boundary is transmitted, and vice versa.
. In other words, any wave energy which is not reflected
at the boundary is transmitted, and vice versa.
Figure 56:
 |
Let us now consider the case of incidence oblique to the boundary (see Fig. 56).
Suppose that the incident wave subtends an angle 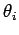 with the
normal to the boundary, whereas the reflected and transmitted
waves subtend angles
with the
normal to the boundary, whereas the reflected and transmitted
waves subtend angles 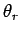 and
and 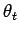 , respectively.
, respectively.
The incident wave can be written
with analogous expressions for the reflected and transmitted waves.
Since, in the case of oblique incidence, the electric and magnetic
components of the wave fields are no longer necessarily parallel to the
boundary, the boundary conditions (1221) and (1222) at 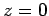 must
be supplemented by the additional boundary conditions
must
be supplemented by the additional boundary conditions
Equation (1235) derives from the general
boundary condition
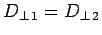 .
.
It follows from Eqs. (1222) and (1236) that both components
of the magnetic field are continuous at the boundary. Hence, we can write
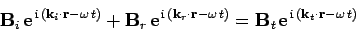 |
(1237) |
at 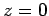 . Given that
. Given that  ,
, 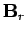 , and
, and 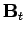 are
constant vectors, the only way in which the above equation can be satisfied for all
values of
are
constant vectors, the only way in which the above equation can be satisfied for all
values of  and
and  is if
is if
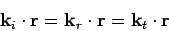 |
(1238) |
throughout the 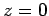 plane. This, in turn, implies that
plane. This, in turn, implies that
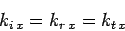 |
(1239) |
and
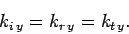 |
(1240) |
It immediately follows that if 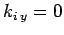 then
then
 .
In other words, if the incident wave lies in the
.
In other words, if the incident wave lies in the  -
- plane then the
reflected and transmitted waves also lie in the
plane then the
reflected and transmitted waves also lie in the  -
- plane. Another
way of putting this is that the incident, reflected, and transmitted
waves all lie in the same plane, know as the plane
of incidence. This, of course, is one of the laws of geometric optics.
From now on, we shall assume that the plane of incidence is the
plane. Another
way of putting this is that the incident, reflected, and transmitted
waves all lie in the same plane, know as the plane
of incidence. This, of course, is one of the laws of geometric optics.
From now on, we shall assume that the plane of incidence is the  -
- plane.
plane.
Now,
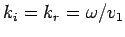 and
and
 . Moreover,
. Moreover,
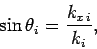 |
(1241) |
with similar expressions for 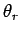 and
and 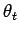 . Hence, according
to Eq. (1239),
. Hence, according
to Eq. (1239),
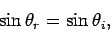 |
(1242) |
which implies that
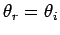 . Moreover,
. Moreover,
 |
(1243) |
Of course, the above expressions correspond to the law of reflection
and Snell's law of refraction, respectively.
For the case of oblique incidence, we need to consider two independent
wave polarizations separately. The first polarization
has all the wave electric fields perpendicular to the plane of incidence, whilst
the second has all the wave magnetic fields perpendicular to the plane
of incidence.
Let us consider the first wave polarization. We can write unit vectors
in the directions of propagation of the incident, reflected, and transmitted
waves likso:
The constant vectors associated with the incident wave are written
where use has been made of Eq. (1214). Likewise, the constant
vectors associated with the reflected and transmitted waves are
and
respectively.
Now, the boundary condition (1221) yields
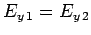 ,
or
,
or
 |
(1253) |
Likewise, the boundary condition (1236) gives
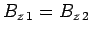 ,
or
,
or
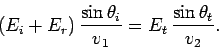 |
(1254) |
However, using Snell's law, (1243), the above expression reduces to Eq. (1253). Finally, the boundary condition (1222) yields
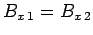 , or
, or
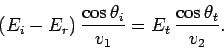 |
(1255) |
It is convenient to define the parameters
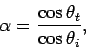 |
(1256) |
and
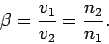 |
(1257) |
Equations (1253) and (1255) can be solved in terms
of these parameters to give
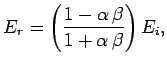 |
|
|
(1258) |
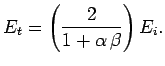 |
|
|
(1259) |
These relations are known as Fresnel equations.
The wave intensity in the  -direction is given by
-direction is given by
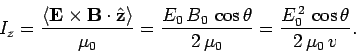 |
(1260) |
Hence, the coefficient of reflection is written
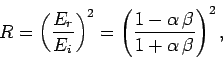 |
(1261) |
whereas the coefficient of transmission takes the form
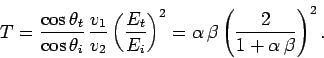 |
(1262) |
Note that it is again the case that 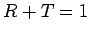 .
.
Let us now consider the second wave polarization. In this case, the
constant vectors associated with the incident, reflected, and transmitted
waves are written
and
and
respectively.
The boundary condition (1222) yields
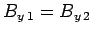 , or
, or
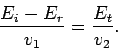 |
(1269) |
Likewise, the boundary condition (1221) gives
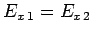 , or
, or
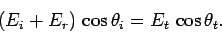 |
(1270) |
Finally, the boundary condition (1235) yields
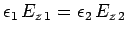 , or
, or
 |
(1271) |
Making use of Snell's law, and the fact that
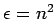 , the
above expression reduces to Eq. (1269).
, the
above expression reduces to Eq. (1269).
Solving Eqs. (1239) and (1270), we obtain
The associated coefficients of reflection and transmission take the
form
respectively. As usual, 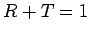 .
.
Note that at oblique incidence the Fresnel equations, (1258) and
(1259), for the wave polarization in which the electric
field is parallel to the boundary are different to the Fresnel equations,
(1272) and (1273), for the wave polarization
in which the magnetic field is parallel to the boundary. This implies that
the coefficients of reflection and transmission for these two wave polarizations
are, in general, different.
Figure 57:
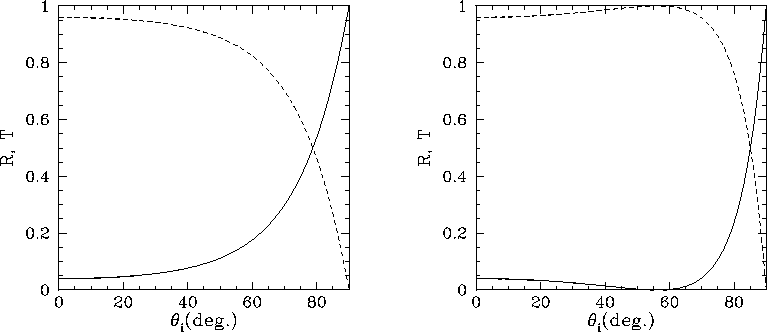 |
Figure 57 shows the coefficients of reflection (solid curves) and transmission
(dashed curves) for oblique incidence from air (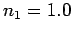 ) to
glass (
) to
glass (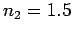 ). The left-hand panel shows the wave polarization
for which the electric field is parallel to the boundary, whereas the
right-hand panel shows the wave polarization for which the
magnetic field is parallel to the boundary. In general, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. Note, however,
that for the second wave polarization there is a particular angle of incidence,
know as the Brewster angle,
at which the reflected intensity is zero. There is no similar behaviour for
the first wave polarization.
). The left-hand panel shows the wave polarization
for which the electric field is parallel to the boundary, whereas the
right-hand panel shows the wave polarization for which the
magnetic field is parallel to the boundary. In general, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. Note, however,
that for the second wave polarization there is a particular angle of incidence,
know as the Brewster angle,
at which the reflected intensity is zero. There is no similar behaviour for
the first wave polarization.
It follows from Eq. (1272) that the Brewster angle corresponds
to the condition
 |
(1276) |
or
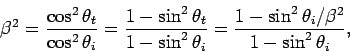 |
(1277) |
where use has been made of Snell's law. The above expression
reduces to
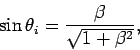 |
(1278) |
or
 . Hence, the Brewster angle satisfies
. Hence, the Brewster angle satisfies
 |
(1279) |
If unpolarized light is incident on an air/glass (say) boundary at the Brewster angle
then the reflected beam is  plane polarized.
plane polarized.



Next: Wave-guides
Up: Electromagnetic radiation
Previous: Dielectric constant of a
Richard Fitzpatrick
2006-02-02
![]() forms the boundary between two different dielectric
media. Let medium 1, of refractive index
forms the boundary between two different dielectric
media. Let medium 1, of refractive index ![]() , occupy the region
, occupy the region ![]() ,
whilst medium 2, of refractive index
,
whilst medium 2, of refractive index ![]() , occupies the region
, occupies the region ![]() .
Let us investigate what happens when an electromagnetic wave is incident
on this boundary from medium 1.
.
Let us investigate what happens when an electromagnetic wave is incident
on this boundary from medium 1.
![]() for the
incident and transmitted waves, and
for the
incident and transmitted waves, and
![]() for the reflected wave. Without loss of generality, we can assume that
the incident wave is polarized in the
for the reflected wave. Without loss of generality, we can assume that
the incident wave is polarized in the ![]() -direction.
Hence, using Eq. (1214), the incident
wave can be written
-direction.
Hence, using Eq. (1214), the incident
wave can be written
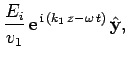
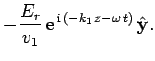

![]() are
are
![]() yields
yields
![]() then
then ![]() and
and ![]() .
In other words, if the two media have the same indices of refraction then
there is no reflection at the boundary between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if
.
In other words, if the two media have the same indices of refraction then
there is no reflection at the boundary between them, and the transmitted
wave is consequently equal in amplitude to the incident wave. On the other
hand, if ![]() then there is some reflection at the boundary. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between
then there is some reflection at the boundary. Indeed,
the amplitude of the reflected wave is roughly proportional to the difference between ![]() and
and ![]() . This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
at an air/glass boundary is reflected, due to the different refractive indicies
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass boundary.
. This has important practical consequences.
We can only see a clean pane of glass in a window because some of the light incident
at an air/glass boundary is reflected, due to the different refractive indicies
of air and glass. As is well-known, it is a lot more difficult to see glass when it is submerged in water. This is because the refractive indices of glass and water are quite similar, and so there is very little reflection of light
incident on a water/glass boundary.
![]() when
when ![]() .
The negative sign indicates a
.
The negative sign indicates a ![]() phase-shift of the reflected wave, with
respect to the incident wave. We conclude that there is a
phase-shift of the reflected wave, with
respect to the incident wave. We conclude that there is a ![]() phase-shift of the reflected wave, relative to the incident wave, on reflection from a boundary with a
medium of greater refractive index. Conversely, there is no
phase-shift
on reflection from a boundary with a medium of lesser refractive index.
phase-shift of the reflected wave, relative to the incident wave, on reflection from a boundary with a
medium of greater refractive index. Conversely, there is no
phase-shift
on reflection from a boundary with a medium of lesser refractive index.
![]() -direction is simply
-direction is simply
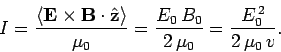
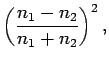
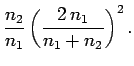
![]() with the
normal to the boundary, whereas the reflected and transmitted
waves subtend angles
with the
normal to the boundary, whereas the reflected and transmitted
waves subtend angles ![]() and
and ![]() , respectively.
, respectively.
![]() and
and
![]() . Moreover,
. Moreover,
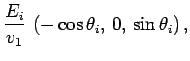

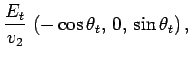
![]() ,
or
,
or
![]() -direction is given by
-direction is given by
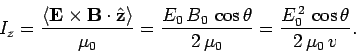
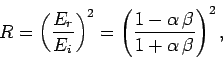
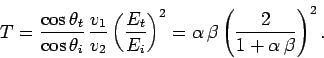

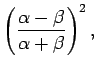
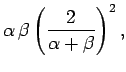
![]() ) to
glass (
) to
glass (![]() ). The left-hand panel shows the wave polarization
for which the electric field is parallel to the boundary, whereas the
right-hand panel shows the wave polarization for which the
magnetic field is parallel to the boundary. In general, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. Note, however,
that for the second wave polarization there is a particular angle of incidence,
know as the Brewster angle,
at which the reflected intensity is zero. There is no similar behaviour for
the first wave polarization.
). The left-hand panel shows the wave polarization
for which the electric field is parallel to the boundary, whereas the
right-hand panel shows the wave polarization for which the
magnetic field is parallel to the boundary. In general, it can
be seen that the coefficient of reflection rises, and the coefficient of
transmission falls, as the angle of incidence increases. Note, however,
that for the second wave polarization there is a particular angle of incidence,
know as the Brewster angle,
at which the reflected intensity is zero. There is no similar behaviour for
the first wave polarization.