


Next: Dielectric constant of a
Up: Electromagnetic radiation
Previous: Faraday rotation
Propagation in a conductor
Consider the propagation of an electromagnetic wave through a conducting
medium which obeys Ohm's law:
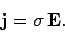 |
(1184) |
Here, 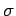 is the conductivity of the medium in question.
Maxwell's equations for the wave take the form:
is the conductivity of the medium in question.
Maxwell's equations for the wave take the form:
 |
 |
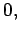 |
(1185) |
 |
 |
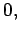 |
(1186) |
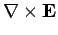 |
 |
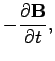 |
(1187) |
 |
 |
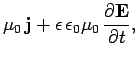 |
(1188) |
where 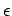 is the dielectric constant of the medium.
It follows, from the above equations, that
is the dielectric constant of the medium.
It follows, from the above equations, that
![\begin{displaymath}
\nabla\times\nabla\times{\bf E} = -\nabla^2{\bf E} = -\frac{...
... \epsilon_0\mu_0 \frac{\partial {\bf E}}{\partial t}\right].
\end{displaymath}](img2397.png) |
(1189) |
Looking for a wave-like solution of the form
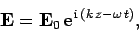 |
(1190) |
we obtain the dispersion relation
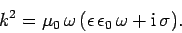 |
(1191) |
Consider a ``poor'' conductor for which
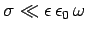 . In this limit, the dispersion relation
(1191) yields
. In this limit, the dispersion relation
(1191) yields
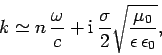 |
(1192) |
where
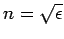 is the refractive index.
Substitution into Eq. (1190) gives
is the refractive index.
Substitution into Eq. (1190) gives
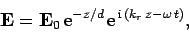 |
(1193) |
where
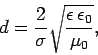 |
(1194) |
and
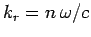 . Thus, we conclude that the amplitude
of an electromagnetic wave propagating through a conductor
decays exponentially on some length-scale,
. Thus, we conclude that the amplitude
of an electromagnetic wave propagating through a conductor
decays exponentially on some length-scale, 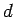 , which
is termed the skin-depth. Note, from Eq. (1194),
that the skin-depth for a poor conductor is independent of the frequency
of the wave. Note, also, that
, which
is termed the skin-depth. Note, from Eq. (1194),
that the skin-depth for a poor conductor is independent of the frequency
of the wave. Note, also, that 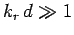 for a poor conductor,
indicating that the wave penetrates many wave-lengths into the
conductor before decaying away.
for a poor conductor,
indicating that the wave penetrates many wave-lengths into the
conductor before decaying away.
Consider a ``good'' conductor for which
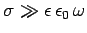 . In this limit, the dispersion relation
(1191) yields
. In this limit, the dispersion relation
(1191) yields
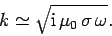 |
(1195) |
Substitution into Eq. (1190) again gives Eq. (1193),
with
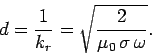 |
(1196) |
It can be seen that the skin-depth for a good conductor decreases
with increasing wave frequency. The fact that 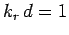 indicates
that the wave only penetrates a few wave-lengths into the conductor
before decaying away.
indicates
that the wave only penetrates a few wave-lengths into the conductor
before decaying away.
Now the power per unit volume dissipated via ohmic heating in
a conducting medium takes the form
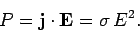 |
(1197) |
Consider an electromagnetic wave of the form (1193). The mean power dissipated
per unit area in the region 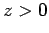 is written
is written
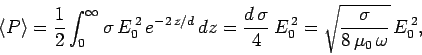 |
(1198) |
for a good conductor.
Now, according to Eq. (1165), the mean electromagnetic
power flux into the region 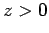 takes the form
takes the form
 |
(1199) |
It is clear, from a comparison of the previous two equations, that
all of the wave energy which flows into the region 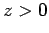 is dissipated via ohmic
heating. We thus conclude that the attenuation of an electromagnetic
wave propagating through a conductor is a direct consequence of ohmic power losses.
is dissipated via ohmic
heating. We thus conclude that the attenuation of an electromagnetic
wave propagating through a conductor is a direct consequence of ohmic power losses.
Consider a typical metallic conductor such as copper, whose electrical
conductivity at room temperature is about
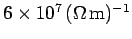 . Copper, therefore, acts as a good
conductor for all electromagnetic waves of frequency below about
. Copper, therefore, acts as a good
conductor for all electromagnetic waves of frequency below about
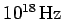 . The skin-depth in copper for such waves is thus
. The skin-depth in copper for such waves is thus
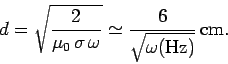 |
(1200) |
It follows that the skin-depth is about 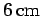 at 1Hz, but only about
2mm at 1kHz. This gives rise to the so-called skin-effect in copper wires, by which an oscillating electromagnetic
signal of increasing frequency, transmitted along such a wire, is confined
to an increasingly narrow layer (whose thickness is of order the skin-depth)
on the surface of the wire.
at 1Hz, but only about
2mm at 1kHz. This gives rise to the so-called skin-effect in copper wires, by which an oscillating electromagnetic
signal of increasing frequency, transmitted along such a wire, is confined
to an increasingly narrow layer (whose thickness is of order the skin-depth)
on the surface of the wire.
The conductivity of sea water is only about
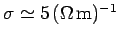 . However, this is still sufficiently high for sea water to act as
a good conductor for all radio frequency electromagnetic waves (i.e.,
. However, this is still sufficiently high for sea water to act as
a good conductor for all radio frequency electromagnetic waves (i.e., 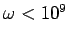 Hz). The skin-depth at 1MHz (
Hz). The skin-depth at 1MHz (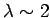 km)
is about
km)
is about 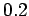 m, whereas that at 1kHz (
m, whereas that at 1kHz (
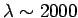 km)
is still only about 7m. This obviously poses quite severe restrictions for
radio communication with submerged submarines. Either the submarines
have to come quite close to the surface to communicate (which is dangerous), or the communication must be performed with extremely low frequency (ELF) waves (i.e.,
km)
is still only about 7m. This obviously poses quite severe restrictions for
radio communication with submerged submarines. Either the submarines
have to come quite close to the surface to communicate (which is dangerous), or the communication must be performed with extremely low frequency (ELF) waves (i.e., 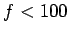 Hz). Unfortunately, such waves have very large wave-lengths (
Hz). Unfortunately, such waves have very large wave-lengths (
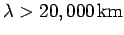 ), which means
that they can only be efficiently generated by extremely large
antennas.
), which means
that they can only be efficiently generated by extremely large
antennas.



Next: Dielectric constant of a
Up: Electromagnetic radiation
Previous: Faraday rotation
Richard Fitzpatrick
2006-02-02
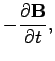
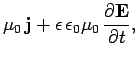
![\begin{displaymath}
\nabla\times\nabla\times{\bf E} = -\nabla^2{\bf E} = -\frac{...
... \epsilon_0\mu_0 \frac{\partial {\bf E}}{\partial t}\right].
\end{displaymath}](img2397.png)
![]() . In this limit, the dispersion relation
(1191) yields
. In this limit, the dispersion relation
(1191) yields
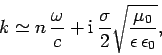
![]() . In this limit, the dispersion relation
(1191) yields
. In this limit, the dispersion relation
(1191) yields
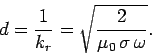
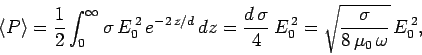

![]() . Copper, therefore, acts as a good
conductor for all electromagnetic waves of frequency below about
. Copper, therefore, acts as a good
conductor for all electromagnetic waves of frequency below about
![]() . The skin-depth in copper for such waves is thus
. The skin-depth in copper for such waves is thus
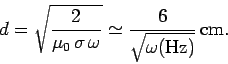
![]() . However, this is still sufficiently high for sea water to act as
a good conductor for all radio frequency electromagnetic waves (i.e.,
. However, this is still sufficiently high for sea water to act as
a good conductor for all radio frequency electromagnetic waves (i.e., ![]() Hz). The skin-depth at 1MHz (
Hz). The skin-depth at 1MHz (![]() km)
is about
km)
is about ![]() m, whereas that at 1kHz (
m, whereas that at 1kHz (
![]() km)
is still only about 7m. This obviously poses quite severe restrictions for
radio communication with submerged submarines. Either the submarines
have to come quite close to the surface to communicate (which is dangerous), or the communication must be performed with extremely low frequency (ELF) waves (i.e.,
km)
is still only about 7m. This obviously poses quite severe restrictions for
radio communication with submerged submarines. Either the submarines
have to come quite close to the surface to communicate (which is dangerous), or the communication must be performed with extremely low frequency (ELF) waves (i.e., ![]() Hz). Unfortunately, such waves have very large wave-lengths (
Hz). Unfortunately, such waves have very large wave-lengths (
![]() ), which means
that they can only be efficiently generated by extremely large
antennas.
), which means
that they can only be efficiently generated by extremely large
antennas.