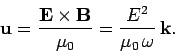Next: Faraday rotation
Up: Electromagnetic radiation
Previous: Dielectric constant of a
Dielectric constant of a plasma
A plasma is very similar to a gaseous medium, expect that the electrons
are free: i.e., there is no restoring force due to nearby atomic
nuclii. Hence, we can obtain an expression for the dielectric constant
of a plasma from Eq. (1149) by setting 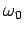 to zero,
and
to zero,
and 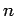 to the number density of electrons,
to the number density of electrons, 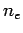 .
We obtain
.
We obtain
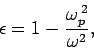 |
(1150) |
where the characteristic frequency
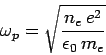 |
(1151) |
is called the plasma frequency.
We can immediately see that formula (1150) is problematic.
For frequencies above the plasma frequency, the dielectric constant
of a plasma is less than unity. Hence, the refractive
index
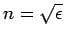 is also less than unity. This would seem to imply that
high frequency electromagnetic waves can propagate through a plasma with
a velocity
is also less than unity. This would seem to imply that
high frequency electromagnetic waves can propagate through a plasma with
a velocity 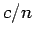 which is greater than the velocity of
light in a vacuum. Does this violate the principles of relativity?
On the other hand, for frequencies below the plasma frequency, the dielectric constant
is negative, which would seem to imply that the refractive
index
which is greater than the velocity of
light in a vacuum. Does this violate the principles of relativity?
On the other hand, for frequencies below the plasma frequency, the dielectric constant
is negative, which would seem to imply that the refractive
index
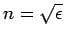 is imaginary. How should we interpret this?
is imaginary. How should we interpret this?
Consider an infinite plane-wave, of frequency, 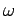 , greater than
the plasma frequency, propagating through a plasma. Suppose that
the wave electric field takes the form
, greater than
the plasma frequency, propagating through a plasma. Suppose that
the wave electric field takes the form
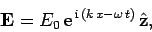 |
(1152) |
where it is understood that the physical electric field is the real
part of the above expression. A peak or trough of the above wave
travels at the so-called phase velocity, which is given by
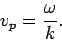 |
(1153) |
Now, we have also seen that the phase velocity of electromagnetic waves
in a dielectric medium is
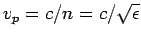 , so
, so
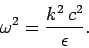 |
(1154) |
It follows from Eq. (1150) that
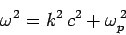 |
(1155) |
in a plasma. The above type of expression, which effectively determines the wave
frequency, 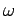 , as a function of the wave-number,
, as a function of the wave-number, 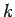 , for the
medium in question, is called a dispersion relation (since,
amongst other things, it determines how fast wave-pulses disperse in
the medium). According to the above dispersion relation, the phase velocity
of high frequency waves propagating through a plasma is given by
, for the
medium in question, is called a dispersion relation (since,
amongst other things, it determines how fast wave-pulses disperse in
the medium). According to the above dispersion relation, the phase velocity
of high frequency waves propagating through a plasma is given by
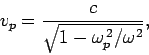 |
(1156) |
which is indeed greater than 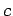 . However, the theory of relativity does not
forbid this. What the theory of relativity says is that information
cannot travel at a velocity greater than
. However, the theory of relativity does not
forbid this. What the theory of relativity says is that information
cannot travel at a velocity greater than 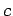 . And the peaks and
troughs of an infinite
plane-wave, such as (1152), do not carry any information.
. And the peaks and
troughs of an infinite
plane-wave, such as (1152), do not carry any information.
We now need to consider how we could transmit information through
a plasma (or any other dielectric medium) by means of electromagnetic
waves. The easiest way would be to send a series of short discrete wave-pulses
through the plasma, so that we could encode information in a sort of
Morse code. We can build up a wave-pulse from a suitable
superposition of infinite plane-waves of different frequencies and
wave-lengths: e.g.,
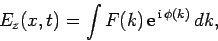 |
(1157) |
where
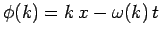 , and
, and
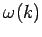 is determined from the dispersion relation
(1155). Now, it turns out that a relatively short wave-pulse can only be built up
from a superposition of plane-waves with a relatively wide range of different
is determined from the dispersion relation
(1155). Now, it turns out that a relatively short wave-pulse can only be built up
from a superposition of plane-waves with a relatively wide range of different 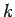 values. Hence, for a short wave-pulse, the integrand in the above formula
consists of the product of a fairly slowly varying function,
values. Hence, for a short wave-pulse, the integrand in the above formula
consists of the product of a fairly slowly varying function, 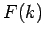 , and
a rapidly oscillating function,
, and
a rapidly oscillating function,
![$\exp[{\rm i} \phi(k)]$](img2339.png) . The latter function
is rapidly oscillating because the phase
. The latter function
is rapidly oscillating because the phase 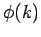 varies very rapidly with
varies very rapidly with 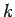 ,
relative to
,
relative to 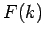 .
We expect the net result of integrating the product of a slowly varying function and rapidly oscillating function to be small, since the oscillations will generally average to zero. It follows that the integral
(1157) is dominated by those regions of
.
We expect the net result of integrating the product of a slowly varying function and rapidly oscillating function to be small, since the oscillations will generally average to zero. It follows that the integral
(1157) is dominated by those regions of 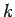 -space for which
-space for which
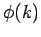 varies least rapidly with
varies least rapidly with 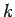 . Hence, the peak of the wave-pulse
most likely corresponds to a maximum or minimum of
. Hence, the peak of the wave-pulse
most likely corresponds to a maximum or minimum of 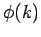 :
i.e.,
:
i.e.,
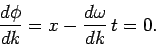 |
(1158) |
Thus, we infer that the velocity of the wave-pulse (which corresponds to the velocity of the peak) is given by
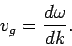 |
(1159) |
This velocity is called the group velocity, and is different to the
phase velocity in dispersive media, for which 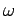 is not directly
proportional to
is not directly
proportional to 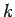 . (Of course, in a vacuum,
. (Of course, in a vacuum, 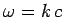 , and both the
phase and group velocities are equal to
, and both the
phase and group velocities are equal to 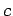 .) The upshot of the above discussion is that information (i.e., an individual wave-pulse)
travels through a dispersive media at the group velocity, rather than the
phase velocity. Hence, relativity demands that the group velocity, rather
than the phase velocity, must
always be less than
.) The upshot of the above discussion is that information (i.e., an individual wave-pulse)
travels through a dispersive media at the group velocity, rather than the
phase velocity. Hence, relativity demands that the group velocity, rather
than the phase velocity, must
always be less than 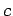 .
.
What is the group velocity for high frequency waves propagating through a plasma?
Well, differentiation of the dispersion relation (1155) yields
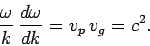 |
(1160) |
Hence, it follows from Eq. (1156) that
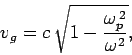 |
(1161) |
which is less than 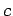 . We thus conclude that the dispersion relation (1155)
is indeed consistent with relativity.
. We thus conclude that the dispersion relation (1155)
is indeed consistent with relativity.
Let us now consider the propagation of low frequency electromagnetic waves through a plasma. We can see, from Eqs. (1156) and (1161),
that when the wave frequency, 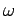 , falls below the plasma frequency,
, falls below the plasma frequency,
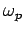 , both the phase and group velocities become imaginary.
This indicates that the wave attenuates as it propagates.
Consider, for instance, a plane-wave of frequency
, both the phase and group velocities become imaginary.
This indicates that the wave attenuates as it propagates.
Consider, for instance, a plane-wave of frequency
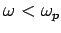 .
According to the dispersion relation (1155), the associated
wave-number is given by
.
According to the dispersion relation (1155), the associated
wave-number is given by
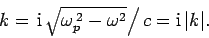 |
(1162) |
Hence, the wave electric field takes the form
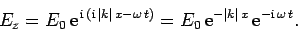 |
(1163) |
Indeed, it can be seen that for
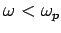 electromagnetic
waves in a plasma take the form of decaying standing waves, rather than
traveling waves. We conclude that an electromagnetic wave, of frequency
less than the plasma frequency, which is incident on a plasma
will not propagate through the plasma. Instead, it will be totally
reflected.
electromagnetic
waves in a plasma take the form of decaying standing waves, rather than
traveling waves. We conclude that an electromagnetic wave, of frequency
less than the plasma frequency, which is incident on a plasma
will not propagate through the plasma. Instead, it will be totally
reflected.
We can be sure that the incident wave is reflected by the plasma, rather than absorbed,
by considering the energy flux of the wave in the plasma.
It is easily demonstrated that the energy flux of an electromagnetic
wave can be written
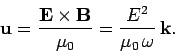 |
(1164) |
For a wave with a real frequency and a complex 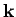 -vector, the
above formula generalizes to
-vector, the
above formula generalizes to
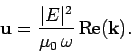 |
(1165) |
However, according to Eq. (1162), the 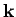 -vector
for a low frequency electromagnetic wave in a plasma is purely
imaginary. It follows that the associated energy flux is zero.
Hence, any low frequency wave which is incident on the plasma
must be totally reflected, since if there were any absorption of the wave
energy
then there would be a net energy flux into the plasma.
-vector
for a low frequency electromagnetic wave in a plasma is purely
imaginary. It follows that the associated energy flux is zero.
Hence, any low frequency wave which is incident on the plasma
must be totally reflected, since if there were any absorption of the wave
energy
then there would be a net energy flux into the plasma.
The outermost layer of the Earth's atmosphere consists of a partially ionized
zone known as the ionosphere. The plasma frequency in the
ionosphere is about 1MHz, which lies at the upper end of the
medium-wave band of radio frequencies. It follows that low
frequency radio signals (i.e., all signals in the long-wave band,
and most in the medium-wave band) are reflected off the ionosphere.
For this reason, such signals can be detected over the horizon. Indeed,
long-wave radio signals reflect multiple times off the ionosphere, with very little loss (they also
reflect multiple times off the Earth, which is enough of a conductor
to act as a mirror for radio waves), and can consequently be detected all over the world.
On the other hand, high frequency radio signals (i.e., all
signals in the FM band) pass straight through the ionosphere. For this
reason, such signals cannot be detected over the horizon, which accounts
for the relatively local coverage of FM radio stations. Note, from
Eq. (1151), that the plasma frequency is proportional to the
square root of the number density of free electrons. Now, the
level of ionization in the ionosphere is maintained by ultra-violet light from the Sun (which effectively knocks electrons out of neutral atoms). Of course, there
is no such light at night, and the number density of free electrons in the
ionosphere consequently drops as electrons and ions gradually recombine.
It follows that the plasma frequency in the ionosphere also drops at night, giving
rise to a marked deterioration in the reception of distant medium-wave radio stations.



Next: Faraday rotation
Up: Electromagnetic radiation
Previous: Dielectric constant of a
Richard Fitzpatrick
2006-02-02
![]() , greater than
the plasma frequency, propagating through a plasma. Suppose that
the wave electric field takes the form
, greater than
the plasma frequency, propagating through a plasma. Suppose that
the wave electric field takes the form
![]() , falls below the plasma frequency,
, falls below the plasma frequency,
![]() , both the phase and group velocities become imaginary.
This indicates that the wave attenuates as it propagates.
Consider, for instance, a plane-wave of frequency
, both the phase and group velocities become imaginary.
This indicates that the wave attenuates as it propagates.
Consider, for instance, a plane-wave of frequency
![]() .
According to the dispersion relation (1155), the associated
wave-number is given by
.
According to the dispersion relation (1155), the associated
wave-number is given by