


Next: Dielectric constant of a
Up: Electromagnetic radiation
Previous: Propagation in a dielectric
Dielectric constant of a gaseous medium
In Sect. 9.5, we discussed a rather crude model of an atom interacting with an electromagnetic wave. According to
this model, the dipole moment 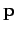 of the atom induced by the wave electric field
of the atom induced by the wave electric field 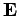 is given by
is given by
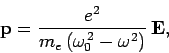 |
(1147) |
where 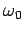 is the natural frequency of the atom (i.e.,
the frequency of one of the atom's spectral lines), and
is the natural frequency of the atom (i.e.,
the frequency of one of the atom's spectral lines), and 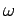 the frequency of the incident radiation. Suppose that there
are
the frequency of the incident radiation. Suppose that there
are 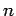 atoms per unit volume. It follows that the induced dipole
moment per unit volume of the assemblage of atoms takes the
form
atoms per unit volume. It follows that the induced dipole
moment per unit volume of the assemblage of atoms takes the
form
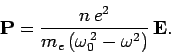 |
(1148) |
Finally, a comparison with Eq. (1139) yields the following expression
for the dielectric constant of the collection of atoms,
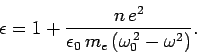 |
(1149) |
The above formula works fairly well for dilute gases, although it is,
of course, necessary to sum over all species and all important
spectral lines.
Note that, in general, the dielectric ``constant'' of a gaseous medium
(as far as electromagnetic radiation is concerned)
is a function of the wave frequency, 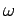 . Since the effective wave
speed through the medium is
. Since the effective wave
speed through the medium is
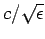 , it follows that
waves of different frequencies traveling through
a gaesous medium do so at different speeds. This phenomenon
is called dispersion, since it can be shown to cause short
wave-pulses to spread out as they propagate through the medium.
At low frequencies (
, it follows that
waves of different frequencies traveling through
a gaesous medium do so at different speeds. This phenomenon
is called dispersion, since it can be shown to cause short
wave-pulses to spread out as they propagate through the medium.
At low frequencies (
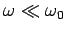 ), however, our
expression for
), however, our
expression for 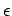 becomes frequency independent, so there
is no dispersion of low frequency waves by a gaseous medium.
becomes frequency independent, so there
is no dispersion of low frequency waves by a gaseous medium.



Next: Dielectric constant of a
Up: Electromagnetic radiation
Previous: Propagation in a dielectric
Richard Fitzpatrick
2006-02-02
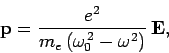
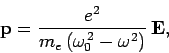
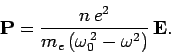
![]() . Since the effective wave
speed through the medium is
. Since the effective wave
speed through the medium is
![]() , it follows that
waves of different frequencies traveling through
a gaesous medium do so at different speeds. This phenomenon
is called dispersion, since it can be shown to cause short
wave-pulses to spread out as they propagate through the medium.
At low frequencies (
, it follows that
waves of different frequencies traveling through
a gaesous medium do so at different speeds. This phenomenon
is called dispersion, since it can be shown to cause short
wave-pulses to spread out as they propagate through the medium.
At low frequencies (
![]() ), however, our
expression for
), however, our
expression for ![]() becomes frequency independent, so there
is no dispersion of low frequency waves by a gaseous medium.
becomes frequency independent, so there
is no dispersion of low frequency waves by a gaseous medium.