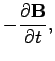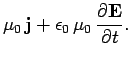Next: Dielectric constant of a
Up: Electromagnetic radiation
Previous: Rayleigh scattering
Consider the propagation of an electromagnetic wave through a
uniform dielectric medium of dielectric constant 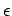 .
According to Eqs. (810) and (812), the dipole moment
per unit volume induced in the medium by the wave electric field
.
According to Eqs. (810) and (812), the dipole moment
per unit volume induced in the medium by the wave electric field 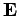 is
is
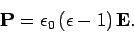 |
(1139) |
There are no free charges or free currents in the medium. There is also
no bound charge density (since the medium is uniform), and no magnetization
current density (since the medium is non-magnetic). However, there
is a polarization current due to the time-variation of the induced
dipole moment per unit volume. According to Eq. (859), this
current is given by
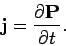 |
(1140) |
Hence, Maxwell's equations take the form
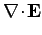 |
 |
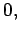 |
(1141) |
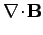 |
 |
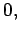 |
(1142) |
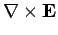 |
 |
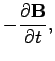 |
(1143) |
 |
 |
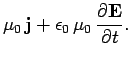 |
(1144) |
According to Eqs. (1139) and (1140), the last of the above
equations can be rewritten
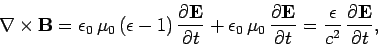 |
(1145) |
since
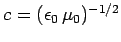 .
Thus, Maxwell's equations for the propagation of electromagnetic waves
through a dielectric medium are the same as Maxwell's equations
for the propagation of waves through a vacuum (see Sect. 4.7), except that
.
Thus, Maxwell's equations for the propagation of electromagnetic waves
through a dielectric medium are the same as Maxwell's equations
for the propagation of waves through a vacuum (see Sect. 4.7), except that
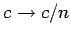 ,
where
,
where
 |
(1146) |
is called the refractive index of the medium in question. Hence,
we conclude that electromagnetic waves propagate through a dielectric
medium slower than through a vacuum by a factor 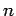 (assuming,
of course, that
(assuming,
of course, that 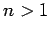 ). This conclusion (which was reached
long before Maxwell's equations were invented) is the basis of all
geometric optics involving refraction.
). This conclusion (which was reached
long before Maxwell's equations were invented) is the basis of all
geometric optics involving refraction.



Next: Dielectric constant of a
Up: Electromagnetic radiation
Previous: Rayleigh scattering
Richard Fitzpatrick
2006-02-02