| (1132) |
We can easily solve Eq. (1132) to give
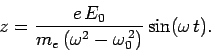 |
(1133) |
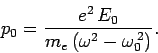 |
(1134) |
In the limit in which the frequency of the incident radiation is much greater
than the natural frequency of the atom, Eqs. (1135) and (1136)
reduce to the previously obtained expressions for scattering by
a free electron. In other words, an electron in an atom acts very much
like a free electron as far as high frequency radiation is concerned.
In the opposite limit, in which the frequency of the incident radiation
is much less than the natural frequency of the atom, Eqs. (1135) and (1136) yield
 |
(1137) |
The most common example of Rayleigh scattering is the scattering
of visible radiation from the Sun by neutral atoms (mostly Nitrogen and Oxygen) in the upper
atmosphere. The frequency of visible radiation is much less than the
typical emission frequencies of a Nitrogen or Oxygen atom (which lie in the
ultra-violet band), so it is certainly the case that
![]() .
When the Sun is low in the sky, radiation from it has to traverse a
comparatively long path through the atmosphere before reaching us. Under
these circumstances, the scattering of direct solar light by neutral atoms in the atmosphere
becomes noticeable (it is not noticeable when the Sun is high is the sky,
and radiation from it consequently only has to traverse a relatively
short path through the atmosphere before reaching us).
According to Eq. (1138), blue light is scattered slightly
more strongly than red light (since blue light has a slightly higher frequency
than red light). Hence, when the Sun is low in the sky, it appears less bright,
due to atmospheric scattering. However, it also appears redder than normal, because
more blue light than red light is scattered out of the solar light-rays, leaving an excess of red light.
Likewise, when we look up at the sky, it does not appear black (like the
sky on the Moon) because of light from solar radiation which grazes
the atmosphere being scattered downward towards the surface of the
Earth. Again, since blue light is scattered more effectively than red light,
there is an excess of blue light scattered downward, and so the sky appears
blue.
.
When the Sun is low in the sky, radiation from it has to traverse a
comparatively long path through the atmosphere before reaching us. Under
these circumstances, the scattering of direct solar light by neutral atoms in the atmosphere
becomes noticeable (it is not noticeable when the Sun is high is the sky,
and radiation from it consequently only has to traverse a relatively
short path through the atmosphere before reaching us).
According to Eq. (1138), blue light is scattered slightly
more strongly than red light (since blue light has a slightly higher frequency
than red light). Hence, when the Sun is low in the sky, it appears less bright,
due to atmospheric scattering. However, it also appears redder than normal, because
more blue light than red light is scattered out of the solar light-rays, leaving an excess of red light.
Likewise, when we look up at the sky, it does not appear black (like the
sky on the Moon) because of light from solar radiation which grazes
the atmosphere being scattered downward towards the surface of the
Earth. Again, since blue light is scattered more effectively than red light,
there is an excess of blue light scattered downward, and so the sky appears
blue.
Light from the Sun is unpolarized. However, when it is scattered it becomes
polarized, because light is scattered preferentially in some directions
rather than others. Consider a light-ray from the Sun which grazes
the Earth's atmosphere. The light-ray contains light which is
polarized such that the electric field is vertical to the ground, and
light which is polarized such that the electric field is horizontal to the ground
(and perpendicular to the path of the light-ray), in equal amounts. However,
due to the ![]() factor in the dipole emission formula
(1119) (where, in this case,
factor in the dipole emission formula
(1119) (where, in this case, ![]() is the angle between the direction of the wave
electric field and the direction of scattering), very little light is scattered downward from the vertically
polarized light compared to the horizontally polarized light.
Moreover, the light scattered from the horizontally polarization is
such that its electric field is preferentially perpendicular, rather than parallel, to the
direction of propagation of the solar light-ray (i.e., the direction to the Sun).
Consequently, the blue light from the sky is preferentially polarized in a direction
perpendicular to the direction to the Sun.
is the angle between the direction of the wave
electric field and the direction of scattering), very little light is scattered downward from the vertically
polarized light compared to the horizontally polarized light.
Moreover, the light scattered from the horizontally polarization is
such that its electric field is preferentially perpendicular, rather than parallel, to the
direction of propagation of the solar light-ray (i.e., the direction to the Sun).
Consequently, the blue light from the sky is preferentially polarized in a direction
perpendicular to the direction to the Sun.