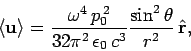Electric dipole radiation

In the previous section, we examined the radiation emitted by a short electric dipole of oscillating dipole moment

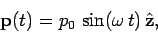$${\bf p}(t) = p_0 \sin(\omega t) \hat{\bf z},$$ (1116)

where $p_0= q_0 l=I_0 l/\omega$. We found that, in the far field, the mean electromagnetic energy flux takes the form [see Eq. (1094)]

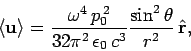$$\langle {\bf u}\rangle = \frac{\omega^4 p_0^{ 2}}{32\pi^2 \epsilon_0 c^3}\frac{\sin^2\theta}{r^2} \hat{\bf r},$$ (1117)

assuming that the dipole is centered on the origin of our spherical polar coordinate system. The mean power radiated into the element of solid angle 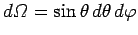$d{\mit\Omega} = \sin\theta d\theta d\varphi$, centered on the angular coordinates (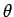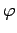$\theta$, $\varphi$), is

$$dP = \langle {\bf u}(r, \theta, \varphi)\rangle\!\cdot\!{\hat{\bf r}} r^2 d{\mit\Omega}.$$ (1118)

Hence, the differential power radiated into this element of solid angle is simply

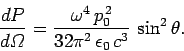$$\frac{dP}{d{\mit\Omega}} = \frac{\omega^4 p_0^{ 2}}{32\pi^2 \epsilon_0 c^3} \sin^2\theta.$$ (1119)

This formula completely specifies the radiation pattern of an oscillating electric dipole (provided that the dipole is much shorter in length than the wave-length of the emitted radiation). Of course, the power radiated into a given element of solid angle is independent of 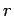$r$, otherwise energy would not be conserved. Finally, the total radiated power is the integral of 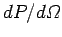$dP/d{\mit\Omega}$ over all solid angles.