


Next: Translational motion versus rotational
Up: Rotational motion
Previous: Torque
Consider a mass  attached to the end of a light rod of length
attached to the end of a light rod of length 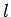 whose
other end is attached to a fixed pivot. Suppose that the pivot is such that the rod
is free to rotate in any direction. Suppose, further, that a force
whose
other end is attached to a fixed pivot. Suppose that the pivot is such that the rod
is free to rotate in any direction. Suppose, further, that a force 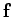 is
applied to the mass, whose instantaneous angular velocity about an axis of rotation passing
through the pivot is
is
applied to the mass, whose instantaneous angular velocity about an axis of rotation passing
through the pivot is
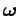 .
.
Let 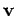 be the instantaneous velocity of the mass. We know that the
rate at which the force
be the instantaneous velocity of the mass. We know that the
rate at which the force 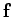 performs work on the mass--otherwise known
as the power--is given by (see Sect. 5.8)
performs work on the mass--otherwise known
as the power--is given by (see Sect. 5.8)
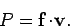 |
(369) |
However, we also know that (see Sect. 8.4)
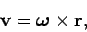 |
(370) |
where  is the vector displacement of the mass from the pivot.
Hence, we can write
is the vector displacement of the mass from the pivot.
Hence, we can write
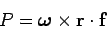 |
(371) |
(note that
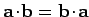 ).
).
Now, for any three vectors,  ,
, 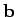 , and
, and 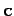 , we can write
, we can write
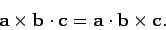 |
(372) |
This theorem is easily proved by expanding the vector and scalar products in component
form using the definitions (319) and (321). It follows
that Eq. (371) can be rewritten
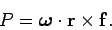 |
(373) |
However,
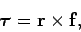 |
(374) |
where
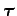 is the torque associated with force
is the torque associated with force 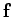 about an axis of rotation passing
through the pivot. Hence, we obtain
about an axis of rotation passing
through the pivot. Hence, we obtain
 |
(375) |
In other words, the rate at which a torque performs work on the object upon which
it acts is the scalar product of the torque and the angular velocity of the object.
Note the great similarity between Eq. (369) and Eq. (375).
Now the relationship between work, 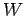 , and power,
, and power, 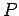 , is simply
, is simply
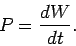 |
(376) |
Likewise, the relationship between angular velocity,
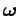 , and angle
of rotation,
, and angle
of rotation,
 , is
, is
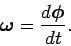 |
(377) |
It follows that Eq. (375) can be rewritten
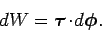 |
(378) |
Integration yields
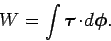 |
(379) |
Note that this is a good definition, since it only involves an infinitesimal
rotation vector,
 . Recall, from Sect. 8.3, that it is impossible
to define a finite rotation vector. For the case of translational motion, the analogous
expression to the above is
. Recall, from Sect. 8.3, that it is impossible
to define a finite rotation vector. For the case of translational motion, the analogous
expression to the above is
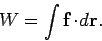 |
(380) |
Here, 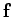 is the force, and
is the force, and 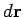 is an element of displacement of the body upon which
the force acts.
is an element of displacement of the body upon which
the force acts.
Although Eqs. (375) and (379) were derived for the special case of
the rotation of a mass attached to the end of a light rod, they are, nevertheless,
completely general.
Consider, finally, the special case in which the torque is aligned with the
angular velocity, and both are constant in time. In this case, the
rate at which the torque performs work is
simply
 |
(381) |
Likewise, the net work performed by the torque in twisting the body upon which
it acts through an angle
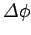 is just
is just
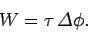 |
(382) |



Next: Translational motion versus rotational
Up: Rotational motion
Previous: Torque
Richard Fitzpatrick
2006-02-02
![]() be the instantaneous velocity of the mass. We know that the
rate at which the force
be the instantaneous velocity of the mass. We know that the
rate at which the force ![]() performs work on the mass--otherwise known
as the power--is given by (see Sect. 5.8)
performs work on the mass--otherwise known
as the power--is given by (see Sect. 5.8)
![]() ,
, ![]() , and
, and ![]() , we can write
, we can write
![]() , and power,
, and power, ![]() , is simply
, is simply