


Next: Centre of mass
Up: Rotational motion
Previous: Is rotation a vector?
The vector product
We saw earlier, in Sect. 3.10, that it is possible to combine two vectors multiplicatively,
by means of a scalar product, to
form a scalar. Recall that the scalar product
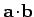 of two vectors
of two vectors
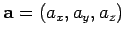 and
and
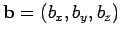 is defined
is defined
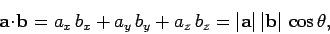 |
(319) |
where  is the angle subtended between the directions of
is the angle subtended between the directions of  and
and 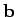 .
.
Is it also possible to combine two vector multiplicatively to form a third (non-coplanar) vector?
It turns out that this goal can be achieved via the use of the so-called
vector product. By definition, the vector product,
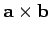 , of two vectors
, of two vectors
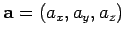 and
and
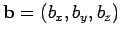 is of
magnitude
is of
magnitude
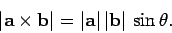 |
(320) |
The direction of
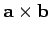 is mutually perpendicular to
is mutually perpendicular to  and
and
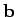 , in the sense given by the right-hand grip rule when vector
, in the sense given by the right-hand grip rule when vector  is rotated onto
vector
is rotated onto
vector 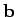 (the direction of rotation being
such that the angle of rotation is less than
(the direction of rotation being
such that the angle of rotation is less than 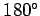 ).
See Fig. 70. In coordinate form,
).
See Fig. 70. In coordinate form,
 |
(321) |
Figure 70:
The vector product.
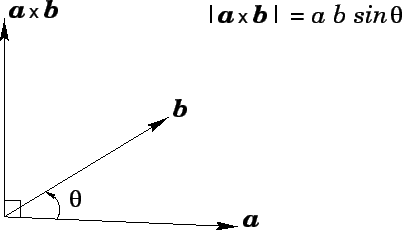 |
There are a number of fairly obvious consequences of the above definition. Firstly, if vector
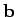 is parallel to vector
is parallel to vector  , so that we can write
, so that we can write
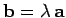 ,
then the vector product
,
then the vector product
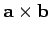 has zero magnitude. The easiest way of seeing
this is to note that if
has zero magnitude. The easiest way of seeing
this is to note that if  and
and 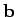 are parallel then the angle
are parallel then the angle  subtended between
them is zero, hence the magnitude of the vector product,
subtended between
them is zero, hence the magnitude of the vector product,
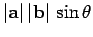 , must
also be zero (since
, must
also be zero (since
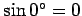 ). Secondly, the order of multiplication matters.
Thus,
). Secondly, the order of multiplication matters.
Thus,
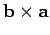 is not equivalent to
is not equivalent to
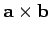 . In fact,
as can be seen from Eq. (321),
. In fact,
as can be seen from Eq. (321),
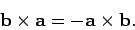 |
(322) |
In other words,
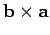 has the same magnitude as
has the same magnitude as
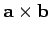 , but
points in diagrammatically the opposite direction.
, but
points in diagrammatically the opposite direction.
Now that we have defined the vector product of two vectors, let us find a use for this concept.
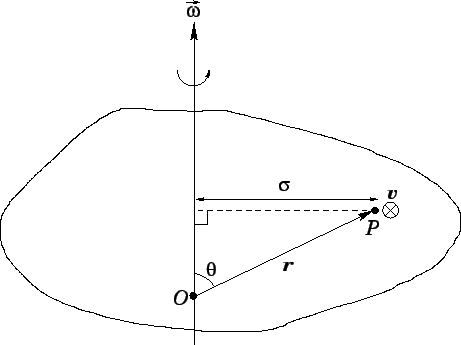
Figure 71 shows a rigid body rotating with angular velocity
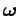 . For the
sake of simplicity, the axis of rotation, which runs parallel to
. For the
sake of simplicity, the axis of rotation, which runs parallel to
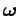 , is
assumed to pass through the origin
, is
assumed to pass through the origin  of our coordinate system. Point
of our coordinate system. Point 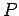 , whose position
vector is
, whose position
vector is  , represents a general point inside the body. What is the velocity
of rotation
, represents a general point inside the body. What is the velocity
of rotation 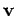 at point
at point 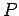 ? Well, the magnitude of this velocity is simply
? Well, the magnitude of this velocity is simply
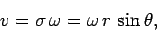 |
(323) |
where 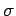 is the perpendicular distance of point
is the perpendicular distance of point 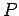 from the axis of rotation, and
from the axis of rotation, and
 is the angle subtended between the directions of
is the angle subtended between the directions of
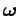 and
and  .
The direction of the velocity is into the page. Another way of saying this, is that the
direction of the velocity is mutually perpendicular to the directions of
.
The direction of the velocity is into the page. Another way of saying this, is that the
direction of the velocity is mutually perpendicular to the directions of
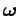 and
and
 , in the sense indicated by the right-hand grip rule when
, in the sense indicated by the right-hand grip rule when
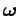 is rotated onto
is rotated onto  (through an angle less than
(through an angle less than 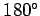 ). It follows that
we can write
). It follows that
we can write
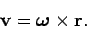 |
(324) |
Note, incidentally,
that the direction of the angular velocity vector
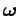 indicates the orientation
of the axis of rotation--however, nothing actually moves in this direction; in fact, all of the motion
is perpendicular to the direction of
indicates the orientation
of the axis of rotation--however, nothing actually moves in this direction; in fact, all of the motion
is perpendicular to the direction of
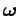 .
.
Figure 71:
Rigid rotation.
 |



Next: Centre of mass
Up: Rotational motion
Previous: Is rotation a vector?
Richard Fitzpatrick
2006-02-02
![]() , of two vectors
, of two vectors
![]() and
and
![]() is of
magnitude
is of
magnitude
![]() is parallel to vector
is parallel to vector ![]() , so that we can write
, so that we can write
![]() ,
then the vector product
,
then the vector product
![]() has zero magnitude. The easiest way of seeing
this is to note that if
has zero magnitude. The easiest way of seeing
this is to note that if ![]() and
and ![]() are parallel then the angle
are parallel then the angle ![]() subtended between
them is zero, hence the magnitude of the vector product,
subtended between
them is zero, hence the magnitude of the vector product,
![]() , must
also be zero (since
, must
also be zero (since
![]() ). Secondly, the order of multiplication matters.
Thus,
). Secondly, the order of multiplication matters.
Thus,
![]() is not equivalent to
is not equivalent to
![]() . In fact,
as can be seen from Eq. (321),
. In fact,
as can be seen from Eq. (321),
![]() . For the
sake of simplicity, the axis of rotation, which runs parallel to
. For the
sake of simplicity, the axis of rotation, which runs parallel to
![]() , is
assumed to pass through the origin
, is
assumed to pass through the origin ![]() of our coordinate system. Point
of our coordinate system. Point ![]() , whose position
vector is
, whose position
vector is ![]() , represents a general point inside the body. What is the velocity
of rotation
, represents a general point inside the body. What is the velocity
of rotation ![]() at point
at point ![]() ? Well, the magnitude of this velocity is simply
? Well, the magnitude of this velocity is simply