


Next: Moment of inertia
Up: Rotational motion
Previous: The vector product
Centre of mass
The centre of mass--or centre of gravity--of an extended object is defined in much
the same manner as we earlier defined the centre of mass of a set of mutually
interacting point mass objects--see Sect. 6.3. To be more exact, the
coordinates of the centre of mass of an extended object are the mass weighted
averages of the coordinates of the elements which make up that object. Thus,
if the object has net mass  , and is composed of
, and is composed of 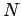 elements,
such that the
elements,
such that the  th element has mass
th element has mass 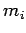 and position vector
and position vector 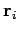 , then the
position vector of the centre of mass is given by
, then the
position vector of the centre of mass is given by
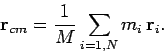 |
(325) |
If the object under consideration is continuous, then
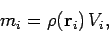 |
(326) |
where 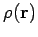 is the mass density of the object, and
is the mass density of the object, and 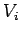 is the volume occupied by the
is the volume occupied by the
 th element. Here, it is assumed that this volume is small compared to the
total volume of the object. Taking the limit that the number of elements goes to
infinity, and the volume of each element goes to zero, Eqs. (325) and (326)
yield the following integral formula for the position vector of the centre of mass:
th element. Here, it is assumed that this volume is small compared to the
total volume of the object. Taking the limit that the number of elements goes to
infinity, and the volume of each element goes to zero, Eqs. (325) and (326)
yield the following integral formula for the position vector of the centre of mass:
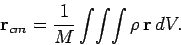 |
(327) |
Here, the integral is taken over the whole volume of the object, and
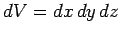 is an element
of that volume. Incidentally, the triple integral sign indicates a volume integral: i.e.,
a simultaneous integral over three independent Cartesian coordinates.
Finally, for an object whose mass density is constant--which is the only type of
object that we shall be considering in this course--the above expression
reduces to
is an element
of that volume. Incidentally, the triple integral sign indicates a volume integral: i.e.,
a simultaneous integral over three independent Cartesian coordinates.
Finally, for an object whose mass density is constant--which is the only type of
object that we shall be considering in this course--the above expression
reduces to
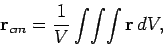 |
(328) |
where 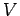 is the volume of the object. According to Eq. (328),
the centre of mass of a body of uniform density is located at the geometric centre of that body.
is the volume of the object. According to Eq. (328),
the centre of mass of a body of uniform density is located at the geometric centre of that body.
Figure 72:
Locating the geometric centre of a cube.
 |
For many solid objects, the location of the geometric centre follows from symmetry.
For instance, the geometric centre of a
cube is the point of intersection of the cube's diagonals. See Fig. 72. Likewise,
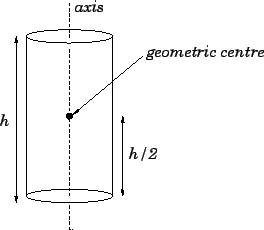
the geometric centre of a right cylinder is located on the axis, half-way up the
cylinder. See Fig. 73.
Figure 73:
Locating the geometric centre of a right cylinder.
 |
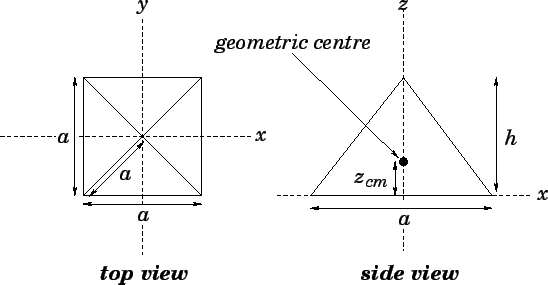
As an illustration of the use of formula (328), let us calculate
the geometric centre of a regular square-sided pyramid. Figure 74 shows such a
pyramid. Let  be the length of each side. It follows, from simple
trigonometry, that the height of
the pyramid is
be the length of each side. It follows, from simple
trigonometry, that the height of
the pyramid is 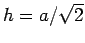 . Suppose that the base of the pyramid lies on the
. Suppose that the base of the pyramid lies on the  -
- plane,
and the apex is aligned with the
plane,
and the apex is aligned with the  -axis, as shown in the diagram.
It follows, from symmetry, that the geometric centre of the pyramid lies on the
-axis, as shown in the diagram.
It follows, from symmetry, that the geometric centre of the pyramid lies on the  -axis.
It only remains to calculate the perpendicular distance,
-axis.
It only remains to calculate the perpendicular distance, 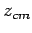 , between the geometric
centre and the base of the pyramid. This quantity is obtained from the
, between the geometric
centre and the base of the pyramid. This quantity is obtained from the  -component
of Eq. (328):
-component
of Eq. (328):
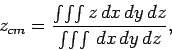 |
(329) |
where the integral is taken over the volume of the pyramid.
Figure 74:
Locating the geometric centre of a regular square-sided pyramid.
 |
In the above integral, the limits of integration for  are
are 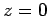 to
to 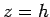 , respectively
(i.e., from the base to the apex of the pyramid).
The corresponding limits of integration for
, respectively
(i.e., from the base to the apex of the pyramid).
The corresponding limits of integration for  and
and  are
are
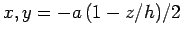 to
to
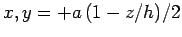 , respectively (i.e., the limits are
, respectively (i.e., the limits are 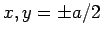 at the
base of the pyramid, and
at the
base of the pyramid, and 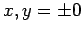 at the apex). Hence, Eq. (329) can
be written more explicitly as
at the apex). Hence, Eq. (329) can
be written more explicitly as
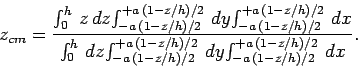 |
(330) |
As indicated above, it makes sense to perform the  - and
- and  - integrals before the
- integrals before the  -integrals,
since the limits of integration for the
-integrals,
since the limits of integration for the  - and
- and  - integrals are
- integrals are  -dependent.
Performing the
-dependent.
Performing the  -integrals, we obtain
-integrals, we obtain
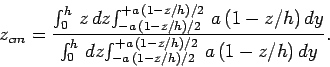 |
(331) |
Performing the  -integrals, we obtain
-integrals, we obtain
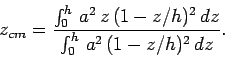 |
(332) |
Finally, performing the  -integrals, we obtain
-integrals, we obtain
![\begin{displaymath}
z_{cm} = \frac{ a^2\left[z^2/2 - 2 z^3/(3 h) + z^4/(4 h^2...
... h)\right]_0^h} = \frac{a^2 h^2/12}{a^2 h/3} = \frac{h}{4}.
\end{displaymath}](img1303.png) |
(333) |
Thus, the geometric centre of a regular square-sided pyramid is located on the
symmetry axis, one quarter of the way from the base to the apex.



Next: Moment of inertia
Up: Rotational motion
Previous: The vector product
Richard Fitzpatrick
2006-02-02
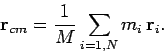
![]() be the length of each side. It follows, from simple
trigonometry, that the height of
the pyramid is
be the length of each side. It follows, from simple
trigonometry, that the height of
the pyramid is ![]() . Suppose that the base of the pyramid lies on the
. Suppose that the base of the pyramid lies on the ![]() -
-![]() plane,
and the apex is aligned with the
plane,
and the apex is aligned with the ![]() -axis, as shown in the diagram.
It follows, from symmetry, that the geometric centre of the pyramid lies on the
-axis, as shown in the diagram.
It follows, from symmetry, that the geometric centre of the pyramid lies on the ![]() -axis.
It only remains to calculate the perpendicular distance,
-axis.
It only remains to calculate the perpendicular distance, ![]() , between the geometric
centre and the base of the pyramid. This quantity is obtained from the
, between the geometric
centre and the base of the pyramid. This quantity is obtained from the ![]() -component
of Eq. (328):
-component
of Eq. (328):
![]() are
are ![]() to
to ![]() , respectively
(i.e., from the base to the apex of the pyramid).
The corresponding limits of integration for
, respectively
(i.e., from the base to the apex of the pyramid).
The corresponding limits of integration for ![]() and
and ![]() are
are
![]() to
to
![]() , respectively (i.e., the limits are
, respectively (i.e., the limits are ![]() at the
base of the pyramid, and
at the
base of the pyramid, and ![]() at the apex). Hence, Eq. (329) can
be written more explicitly as
at the apex). Hence, Eq. (329) can
be written more explicitly as
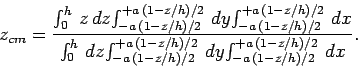
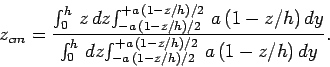
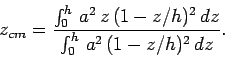
![\begin{displaymath}
z_{cm} = \frac{ a^2\left[z^2/2 - 2 z^3/(3 h) + z^4/(4 h^2...
... h)\right]_0^h} = \frac{a^2 h^2/12}{a^2 h/3} = \frac{h}{4}.
\end{displaymath}](img1303.png)