


Next: Torque
Up: Rotational motion
Previous: Centre of mass
Moment of inertia
Consider an extended object which is made up of 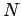 elements. Let the
elements. Let the  th element
possess mass
th element
possess mass 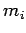 , position vector
, position vector 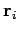 , and velocity
, and velocity 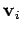 . The
total kinetic energy of the object is written
. The
total kinetic energy of the object is written
 |
(334) |
Suppose that the motion of the object consists merely of rigid rotation at angular
velocity
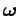 . It follows, from Sect. 8.4, that
. It follows, from Sect. 8.4, that
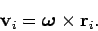 |
(335) |
Let us write
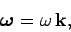 |
(336) |
where 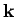 is a unit vector aligned along the axis of rotation (which
is assumed to pass through the origin of our coordinate system). It follows from
the above equations that the kinetic energy of rotation of the object takes the
form
is a unit vector aligned along the axis of rotation (which
is assumed to pass through the origin of our coordinate system). It follows from
the above equations that the kinetic energy of rotation of the object takes the
form
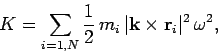 |
(337) |
or
 |
(338) |
Here, the quantity 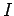 is termed the moment of inertia of the object, and
is written
is termed the moment of inertia of the object, and
is written
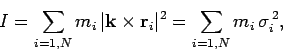 |
(339) |
where
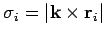 is the perpendicular distance from the
is the perpendicular distance from the  th element to the axis of
rotation. Note that for translational motion we usually write
th element to the axis of
rotation. Note that for translational motion we usually write
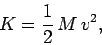 |
(340) |
where  represents mass and
represents mass and  represents speed. A comparison of
Eqs. (338) and (340) suggests that moment of inertia plays the
same role in rotational motion that mass plays in translational motion.
represents speed. A comparison of
Eqs. (338) and (340) suggests that moment of inertia plays the
same role in rotational motion that mass plays in translational motion.
For a continuous object, analogous arguments to those employed in Sect. 8.5
yield
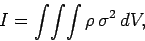 |
(341) |
where 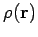 is the mass density of the object,
is the mass density of the object,
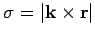 is
the perpendicular distance from the axis of rotation,
and
is
the perpendicular distance from the axis of rotation,
and 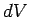 is a volume element.
Finally, for an object of constant density, the above expression reduces to
is a volume element.
Finally, for an object of constant density, the above expression reduces to
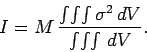 |
(342) |
Here,  is the total mass of the object. Note that the integrals are taken over the whole
volume of the object.
is the total mass of the object. Note that the integrals are taken over the whole
volume of the object.
The moment of inertia of a uniform object depends not only on the size and shape of that
object but on the location of the axis about which the object is rotating. In particular,
the same object can have different moments of inertia when rotating about
different axes.
Unfortunately, the evaluation of the moment of inertia of a given body about a given axis invariably
involves the performance of a nasty volume integral. In fact, there is only
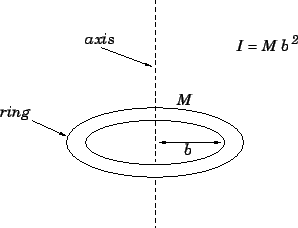
one trivial moment of inertia calculation--namely, the moment of inertia of a thin
circular ring about a symmetric axis which runs perpendicular
to the plane of the ring. See Fig. 75. Suppose that  is the mass of the ring, and
is the mass of the ring, and
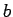 is its radius. Each element of the ring shares a common perpendicular distance from
the axis of rotation--i.e.,
is its radius. Each element of the ring shares a common perpendicular distance from
the axis of rotation--i.e.,  . Hence, Eq. (342)
reduces to
. Hence, Eq. (342)
reduces to
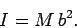 |
(343) |
Figure 75:
The moment of inertia of a ring about a perpendicular symmetric axis.
 |
In general, moments of inertia are rather tedious to calculate. Fortunately, there exist
two powerful theorems which enable us to simply relate the moment of inertia of a given body
about a given axis to the moment of inertia of the same body about another axis. The first of
these theorems is called the perpendicular axis theorem, and only applies to
uniform laminar objects. Consider a laminar object (i.e., a thin, planar object)
of uniform density. Suppose, for the sake of simplicity,
that the object lies in the  -
- plane. The moment of inertia of the object about the
plane. The moment of inertia of the object about the
 -axis is given by
-axis is given by
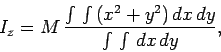 |
(344) |
where we have suppressed the trivial  -integration, and the integral is taken
over the extent of the object in the
-integration, and the integral is taken
over the extent of the object in the  -
- plane. Incidentally, the
above expression follows from the observation that
plane. Incidentally, the
above expression follows from the observation that
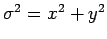 when the axis of rotation is coincident with the
when the axis of rotation is coincident with the  -axis. Likewise, the moments of
inertia of the object about the
-axis. Likewise, the moments of
inertia of the object about the  - and
- and  - axes take the form
- axes take the form
respectively.
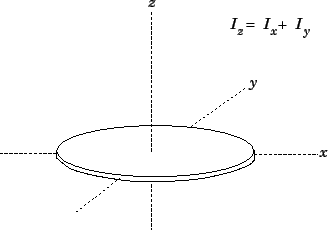
Here, we have made use of the fact that  inside the object. It follows by inspection
of the previous three equations that
inside the object. It follows by inspection
of the previous three equations that
 |
(347) |
See Fig. 76.
Figure 76:
The perpendicular axis theorem.
 |
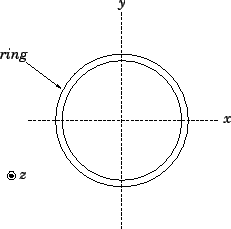
Let us use the perpendicular axis theorem to find the moment of inertia of a thin ring about
a symmetric axis which lies in the plane of the ring. Adopting the coordinate system shown in
Fig. 77, it is clear, from symmetry, that 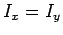 .
Now, we already know that
.
Now, we already know that 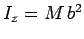 ,
where
,
where  is the mass of the ring, and
is the mass of the ring, and 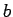 is its radius. Hence, the perpendicular axis
theorem tells us that
is its radius. Hence, the perpendicular axis
theorem tells us that
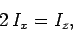 |
(348) |
or
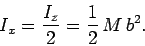 |
(349) |
Of course, 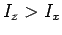 , because when the ring spins about the
, because when the ring spins about the  -axis its elements are, on average,
farther from the axis of rotation than when it spins about the
-axis its elements are, on average,
farther from the axis of rotation than when it spins about the  -axis.
-axis.
Figure 77:
The moment of inertia of a ring about a coplanar symmetric axis.
 |
The second useful theorem regarding moments of inertia is called the parallel
axis theorem. The parallel axis theorem--which is quite general--states that if 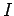 is the moment of inertia of a given body about an axis passing through the centre of mass
of that body, then the moment of inertia
is the moment of inertia of a given body about an axis passing through the centre of mass
of that body, then the moment of inertia  of the same body about a second axis
which is parallel to the first is
of the same body about a second axis
which is parallel to the first is
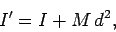 |
(350) |
where  is the mass of the body, and
is the mass of the body, and 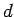 is the perpendicular distance between the
two axes.
is the perpendicular distance between the
two axes.
In order to prove the parallel axis theorem, let us choose the origin of our
coordinate system to coincide with the centre of mass of the body in question.
Furthermore, let us orientate the axes of our coordinate system such that
the  -axis coincides with the first axis of rotation, whereas the second
axis pieces the
-axis coincides with the first axis of rotation, whereas the second
axis pieces the  -
- plane at
plane at 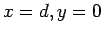 . From Eq. (328), the fact that
the centre of mass is located at the origin implies that
. From Eq. (328), the fact that
the centre of mass is located at the origin implies that
 |
(351) |
where the integrals are taken over the volume of the body. From Eq. (342),
the expression for the first moment of inertia is
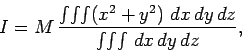 |
(352) |
since 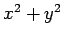 is the perpendicular distance of a general point
is the perpendicular distance of a general point 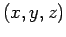 from the
from the  -axis.
Likewise, the expression for the second moment of inertia takes the
form
-axis.
Likewise, the expression for the second moment of inertia takes the
form
![\begin{displaymath}
I' = M \frac{\int\!\int\!\int [(x-d)^2+y^2] dx dy dz}
{\int\!\int\!\int dx dy dz}.
\end{displaymath}](img1342.png) |
(353) |
The above equation can be expanded to give
It follows from Eqs. (351) and (352) that
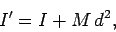 |
(355) |
which proves the theorem.
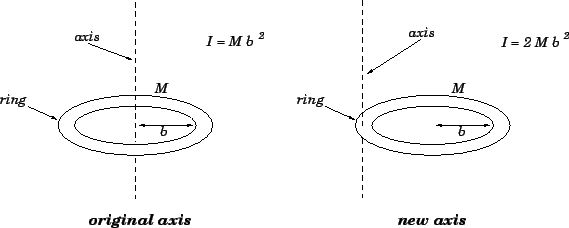
Let us use the parallel axis theorem to calculate the moment of inertia,  , of a thin
ring about an axis which runs perpendicular to the plane of the ring, and passes
through the circumference of the ring. We know that the moment of inertia of a ring of mass
, of a thin
ring about an axis which runs perpendicular to the plane of the ring, and passes
through the circumference of the ring. We know that the moment of inertia of a ring of mass
 and radius
and radius 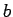 about an axis which runs perpendicular to the plane of the ring, and passes
through the centre of the ring--which coincides with the centre
of mass of the ring--is
about an axis which runs perpendicular to the plane of the ring, and passes
through the centre of the ring--which coincides with the centre
of mass of the ring--is  . Our new axis is parallel to this original axis, but shifted
sideways by the perpendicular distance
. Our new axis is parallel to this original axis, but shifted
sideways by the perpendicular distance 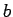 . Hence, the parallel
axis theorem tells us that
. Hence, the parallel
axis theorem tells us that
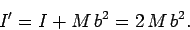 |
(356) |
See Fig. 78.
Figure 78:
An application of the parallel axis theorem.
 |
As an illustration of the direct application of formula (342), let us
calculate the moment of inertia of a thin circular disk, of mass  and radius
and radius 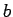 ,
about an axis which passes through the centre of the disk, and runs perpendicular to
the plane of the disk. Let us choose our coordinate system such that the disk
lies in the
,
about an axis which passes through the centre of the disk, and runs perpendicular to
the plane of the disk. Let us choose our coordinate system such that the disk
lies in the  -
- plane with its centre at the origin. The axis of rotation is, therefore,
coincident with the
plane with its centre at the origin. The axis of rotation is, therefore,
coincident with the  -axis. Hence, formula (342) reduces to
-axis. Hence, formula (342) reduces to
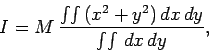 |
(357) |
where the integrals are taken over the area of the disk, and the redundant  -integration
has been suppressed. Let us divide the disk up into thin annuli. Consider an annulus
of radius
-integration
has been suppressed. Let us divide the disk up into thin annuli. Consider an annulus
of radius
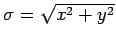 and radial thickness
and radial thickness 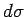 . The area of this annulus is simply
. The area of this annulus is simply
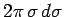 . Hence, we can replace
. Hence, we can replace 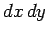 in the above integrals by
in the above integrals by
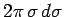 , so as to give
, so as to give
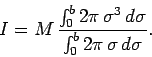 |
(358) |
The above expression yields
![\begin{displaymath}
I = M \frac{\left[2 \pi \sigma^4/4\right]_0^b}{\left[2 \pi \sigma^2/2\right]_0^b}=
\frac{1}{2} M b^2.
\end{displaymath}](img1356.png) |
(359) |
Similar calculations to the above yield the following standard results:
- The moment of inertia of a thin rod of mass
 and length
and length 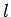 about an axis
passing through the centre of the rod and perpendicular to its length is
about an axis
passing through the centre of the rod and perpendicular to its length is
- The moment of inertia of a thin rectangular sheet of mass
 and dimensions
and dimensions  and
and 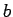 about a perpendicular axis passing through the centre of the sheet is
about a perpendicular axis passing through the centre of the sheet is
- The moment of inertia of a
solid cylinder of mass
 and radius
and radius 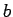 about the cylindrical axis is
about the cylindrical axis is
- The moment of inertia of a
thin spherical shell of mass
 and radius
and radius 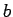 about a diameter is
about a diameter is
- The moment of inertia of a
solid sphere of mass
 and radius
and radius 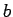 about a diameter is
about a diameter is



Next: Torque
Up: Rotational motion
Previous: Centre of mass
Richard Fitzpatrick
2006-02-02


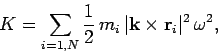
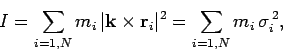
![]() is the mass of the ring, and
is the mass of the ring, and
![]() is its radius. Each element of the ring shares a common perpendicular distance from
the axis of rotation--i.e.,
is its radius. Each element of the ring shares a common perpendicular distance from
the axis of rotation--i.e., ![]() . Hence, Eq. (342)
reduces to
. Hence, Eq. (342)
reduces to
![]() -
-![]() plane. The moment of inertia of the object about the
plane. The moment of inertia of the object about the
![]() -axis is given by
-axis is given by
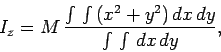
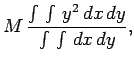

![]() .
Now, we already know that
.
Now, we already know that ![]() ,
where
,
where ![]() is the mass of the ring, and
is the mass of the ring, and ![]() is its radius. Hence, the perpendicular axis
theorem tells us that
is its radius. Hence, the perpendicular axis
theorem tells us that
![]() is the moment of inertia of a given body about an axis passing through the centre of mass
of that body, then the moment of inertia
is the moment of inertia of a given body about an axis passing through the centre of mass
of that body, then the moment of inertia ![]() of the same body about a second axis
which is parallel to the first is
of the same body about a second axis
which is parallel to the first is
![]() -axis coincides with the first axis of rotation, whereas the second
axis pieces the
-axis coincides with the first axis of rotation, whereas the second
axis pieces the ![]() -
-![]() plane at
plane at ![]() . From Eq. (328), the fact that
the centre of mass is located at the origin implies that
. From Eq. (328), the fact that
the centre of mass is located at the origin implies that
![\begin{displaymath}
I' = M \frac{\int\!\int\!\int [(x-d)^2+y^2] dx dy dz}
{\int\!\int\!\int dx dy dz}.
\end{displaymath}](img1342.png)
![$\displaystyle M \frac{\int\!\int\!\int [(x^2+y^2) - 2 d x + d^2] dx dy dz}
{\int\!\int\!\int dx dy dz}$](img1344.png)
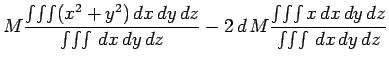
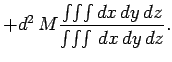
![]() , of a thin
ring about an axis which runs perpendicular to the plane of the ring, and passes
through the circumference of the ring. We know that the moment of inertia of a ring of mass
, of a thin
ring about an axis which runs perpendicular to the plane of the ring, and passes
through the circumference of the ring. We know that the moment of inertia of a ring of mass
![]() and radius
and radius ![]() about an axis which runs perpendicular to the plane of the ring, and passes
through the centre of the ring--which coincides with the centre
of mass of the ring--is
about an axis which runs perpendicular to the plane of the ring, and passes
through the centre of the ring--which coincides with the centre
of mass of the ring--is ![]() . Our new axis is parallel to this original axis, but shifted
sideways by the perpendicular distance
. Our new axis is parallel to this original axis, but shifted
sideways by the perpendicular distance ![]() . Hence, the parallel
axis theorem tells us that
. Hence, the parallel
axis theorem tells us that
![]() and radius
and radius ![]() ,
about an axis which passes through the centre of the disk, and runs perpendicular to
the plane of the disk. Let us choose our coordinate system such that the disk
lies in the
,
about an axis which passes through the centre of the disk, and runs perpendicular to
the plane of the disk. Let us choose our coordinate system such that the disk
lies in the ![]() -
-![]() plane with its centre at the origin. The axis of rotation is, therefore,
coincident with the
plane with its centre at the origin. The axis of rotation is, therefore,
coincident with the ![]() -axis. Hence, formula (342) reduces to
-axis. Hence, formula (342) reduces to
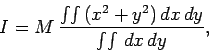
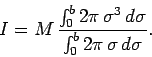
![\begin{displaymath}
I = M \frac{\left[2 \pi \sigma^4/4\right]_0^b}{\left[2 \pi \sigma^2/2\right]_0^b}=
\frac{1}{2} M b^2.
\end{displaymath}](img1356.png)