


Next: The vector product
Up: Rotational motion
Previous: Rigid body rotation
Is rotation a vector?
Consider a rigid body which rotates through an angle 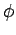 about a given
axis.
It is tempting to try to define a rotation ``vector''
about a given
axis.
It is tempting to try to define a rotation ``vector''
 which describes this
motion. For example, suppose that
which describes this
motion. For example, suppose that
 is defined as the ``vector'' whose magnitude
is the angle of rotation,
is defined as the ``vector'' whose magnitude
is the angle of rotation, 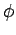 , and whose direction runs parallel to the axis of
rotation. Unfortunately, this definition is ambiguous, since there are
two possible directions which run parallel to the rotation axis. However, we can
resolve this problem by adopting the following convention--the
rotation ``vector'' runs parallel to the axis of rotation in the sense indicated by the
thumb of the right-hand, when the fingers of this hand circulate around the axis in the
direction of rotation. This convention is known as the right-hand grip rule.
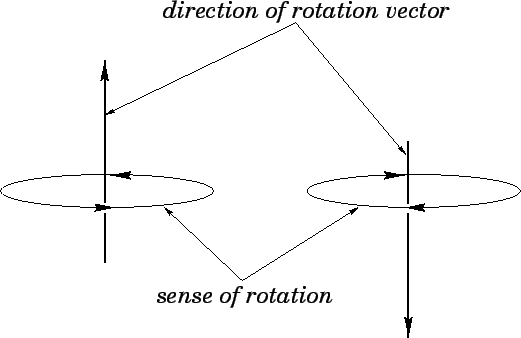
The right-hand grip rule is illustrated in Fig. 68.
, and whose direction runs parallel to the axis of
rotation. Unfortunately, this definition is ambiguous, since there are
two possible directions which run parallel to the rotation axis. However, we can
resolve this problem by adopting the following convention--the
rotation ``vector'' runs parallel to the axis of rotation in the sense indicated by the
thumb of the right-hand, when the fingers of this hand circulate around the axis in the
direction of rotation. This convention is known as the right-hand grip rule.
The right-hand grip rule is illustrated in Fig. 68.
Figure 68:
The right-hand grip rule.
 |
The rotation ``vector''
 now has a well-defined magnitude and
direction. But, is this quantity really a vector?
This may seem like a strange question to ask, but it turns out that not all
quantities which have well-defined magnitudes and directions are necessarily
vectors. Let us review some properties of vectors. If
now has a well-defined magnitude and
direction. But, is this quantity really a vector?
This may seem like a strange question to ask, but it turns out that not all
quantities which have well-defined magnitudes and directions are necessarily
vectors. Let us review some properties of vectors. If  and
and 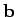 are two general vectors, then it is certainly the case that
are two general vectors, then it is certainly the case that
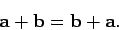 |
(315) |
In other words, the addition of vectors is necessarily commutative (i.e., it is
independent of the order of addition). Is this true for ``vector'' rotations, as we have
just defined them?
Figure 69 shows the effect of applying two successive 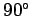 rotations--one about the
rotations--one about the  -axis, and the other about the
-axis, and the other about the  -axis--to a six-sided die. In the
left-hand case, the
-axis--to a six-sided die. In the
left-hand case, the  -rotation is applied before the
-rotation is applied before the  -rotation, and vice
versa in the right-hand case. It can be seen that the die ends up in two completely
different states. Clearly, the
-rotation, and vice
versa in the right-hand case. It can be seen that the die ends up in two completely
different states. Clearly, the  -rotation plus the
-rotation plus the
 -rotation does not equal
the
-rotation does not equal
the  -rotation plus the
-rotation plus the  -rotation. This non-commutative algebra cannot be
represented by vectors. We conclude that, although rotations have well-defined magnitudes and
directions, they are not, in general, vector quantities.
-rotation. This non-commutative algebra cannot be
represented by vectors. We conclude that, although rotations have well-defined magnitudes and
directions, they are not, in general, vector quantities.
Figure 69:
The addition of rotation is non-commutative.
|
There is a direct analogy between rotation and motion over the Earth's surface. After
all, the motion of a pointer along the Earth's equator from longitude 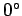 W to
longitude
W to
longitude 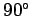 W could just as well be achieved by keeping the pointer fixed and
rotating the Earth through
W could just as well be achieved by keeping the pointer fixed and
rotating the Earth through 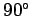 about a North-South axis. The non-commutative nature
of rotation ``vectors'' is a direct consequence of the non-planar (i.e., curved)
nature of the Earth's surface.
For instance, suppose we start off at (
about a North-South axis. The non-commutative nature
of rotation ``vectors'' is a direct consequence of the non-planar (i.e., curved)
nature of the Earth's surface.
For instance, suppose we start off at (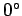 N,
N, 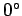 W), which is just off the Atlantic
coast of equatorial Africa, and rotate
W), which is just off the Atlantic
coast of equatorial Africa, and rotate 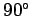 northwards and then
northwards and then 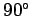 eastwards.
We end up at (
eastwards.
We end up at (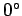 N,
N, 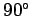 E), which is in the middle of the Indian Ocean. However,
if we start at the same point, and rotate
E), which is in the middle of the Indian Ocean. However,
if we start at the same point, and rotate 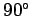 eastwards and then
eastwards and then 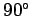 northwards,
we end up at the North pole. Hence, large rotations over the Earth's surface do
not commute.
Let us now repeat this experiment on a far smaller
scale. Suppose that we walk 10m northwards and then 10m eastwards.
Next, suppose that--starting from
the same initial position--we walk 10m eastwards and then 10m northwards. In this case, few people
would need much convincing that the two end points are essentially identical. The
crucial point
is that for sufficiently small displacements the Earth's surface is approximately planar, and
vector displacements on a plane surface commute with one another. This observation immediately
suggests that rotation ``vectors'' which correspond to rotations through small angles
must also commute with
one another. In other words, although the quantity
northwards,
we end up at the North pole. Hence, large rotations over the Earth's surface do
not commute.
Let us now repeat this experiment on a far smaller
scale. Suppose that we walk 10m northwards and then 10m eastwards.
Next, suppose that--starting from
the same initial position--we walk 10m eastwards and then 10m northwards. In this case, few people
would need much convincing that the two end points are essentially identical. The
crucial point
is that for sufficiently small displacements the Earth's surface is approximately planar, and
vector displacements on a plane surface commute with one another. This observation immediately
suggests that rotation ``vectors'' which correspond to rotations through small angles
must also commute with
one another. In other words, although the quantity
 , defined above, is not a true
vector, the infinitesimal quantity
, defined above, is not a true
vector, the infinitesimal quantity
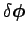 , which is defined in a similar manner but
corresponds to a rotation through an infinitesimal angle
, which is defined in a similar manner but
corresponds to a rotation through an infinitesimal angle 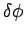 , is a perfectly good
vector.
, is a perfectly good
vector.
We have just established that it is possible to define a true vector
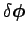 which
describes a rotation through a small angle
which
describes a rotation through a small angle 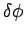 about a fixed axis. But, how is this
definition
useful? Well, suppose that vector
about a fixed axis. But, how is this
definition
useful? Well, suppose that vector
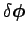 describes the small rotation that a given
object executes in the infinitesimal time interval between
describes the small rotation that a given
object executes in the infinitesimal time interval between  and
and 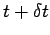 . We can
then define the quantity
. We can
then define the quantity
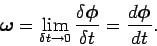 |
(316) |
This quantity is clearly a true vector, since it is simply the ratio of a true vector and
a scalar. Of course,
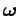 represents an angular velocity vector. The
magnitude of this vector,
represents an angular velocity vector. The
magnitude of this vector,  , specifies the instantaneous angular velocity of the
object, whereas the direction of the vector indicates the axis of rotation. The sense
of rotation is given by the right-hand grip rule: if the thumb of the right-hand points along
the direction of the vector, then the fingers of the right-hand indicate the sense of rotation.
We conclude that, although rotation can only be thought of as a vector quantity under certain
very special circumstances, we can safely treat angular velocity as a vector
quantity under all circumstances.
, specifies the instantaneous angular velocity of the
object, whereas the direction of the vector indicates the axis of rotation. The sense
of rotation is given by the right-hand grip rule: if the thumb of the right-hand points along
the direction of the vector, then the fingers of the right-hand indicate the sense of rotation.
We conclude that, although rotation can only be thought of as a vector quantity under certain
very special circumstances, we can safely treat angular velocity as a vector
quantity under all circumstances.
Suppose, for example, that a rigid body rotates at constant angular velocity
 .
Let us now combine this motion with rotation about a different axis at constant
angular velocity
.
Let us now combine this motion with rotation about a different axis at constant
angular velocity
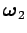 . What is the subsequent motion of the body? Since we know
that angular velocity is a vector, we can be certain that the combined motion simply
corresponds to rotation about a third axis at constant angular velocity
. What is the subsequent motion of the body? Since we know
that angular velocity is a vector, we can be certain that the combined motion simply
corresponds to rotation about a third axis at constant angular velocity
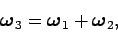 |
(317) |
where the sum is performed according to the standard rules of vector addition. [Note, however,
the following important proviso. In order for Eq. (317) to be valid, the rotation
axes corresponding to
 and
and
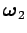 must cross at a certain
point--the rotation axis corresponding to
must cross at a certain
point--the rotation axis corresponding to
 then passes through this point.]
Moreover,
a constant angular velocity
then passes through this point.]
Moreover,
a constant angular velocity
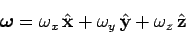 |
(318) |
can be thought of as representing rotation about the  -axis at angular velocity
-axis at angular velocity 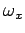 ,
combined with rotation about the
,
combined with rotation about the  -axis at angular velocity
-axis at angular velocity 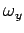 , combined with
rotation about the
, combined with
rotation about the  -axis at angular velocity
-axis at angular velocity 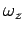 . [There is, again, a proviso--namely,
that the rotation axis corresponding to
. [There is, again, a proviso--namely,
that the rotation axis corresponding to
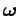 must pass through the origin. Of course,
we can always shift the origin such that this is the case.]
Clearly, the knowledge that
angular velocity is vector quantity can be extremely useful.
must pass through the origin. Of course,
we can always shift the origin such that this is the case.]
Clearly, the knowledge that
angular velocity is vector quantity can be extremely useful.



Next: The vector product
Up: Rotational motion
Previous: Rigid body rotation
Richard Fitzpatrick
2006-02-02

![]() now has a well-defined magnitude and
direction. But, is this quantity really a vector?
This may seem like a strange question to ask, but it turns out that not all
quantities which have well-defined magnitudes and directions are necessarily
vectors. Let us review some properties of vectors. If
now has a well-defined magnitude and
direction. But, is this quantity really a vector?
This may seem like a strange question to ask, but it turns out that not all
quantities which have well-defined magnitudes and directions are necessarily
vectors. Let us review some properties of vectors. If ![]() and
and ![]() are two general vectors, then it is certainly the case that
are two general vectors, then it is certainly the case that
![]() W to
longitude
W to
longitude ![]() W could just as well be achieved by keeping the pointer fixed and
rotating the Earth through
W could just as well be achieved by keeping the pointer fixed and
rotating the Earth through ![]() about a North-South axis. The non-commutative nature
of rotation ``vectors'' is a direct consequence of the non-planar (i.e., curved)
nature of the Earth's surface.
For instance, suppose we start off at (
about a North-South axis. The non-commutative nature
of rotation ``vectors'' is a direct consequence of the non-planar (i.e., curved)
nature of the Earth's surface.
For instance, suppose we start off at (![]() N,
N, ![]() W), which is just off the Atlantic
coast of equatorial Africa, and rotate
W), which is just off the Atlantic
coast of equatorial Africa, and rotate ![]() northwards and then
northwards and then ![]() eastwards.
We end up at (
eastwards.
We end up at (![]() N,
N, ![]() E), which is in the middle of the Indian Ocean. However,
if we start at the same point, and rotate
E), which is in the middle of the Indian Ocean. However,
if we start at the same point, and rotate ![]() eastwards and then
eastwards and then ![]() northwards,
we end up at the North pole. Hence, large rotations over the Earth's surface do
not commute.
Let us now repeat this experiment on a far smaller
scale. Suppose that we walk 10m northwards and then 10m eastwards.
Next, suppose that--starting from
the same initial position--we walk 10m eastwards and then 10m northwards. In this case, few people
would need much convincing that the two end points are essentially identical. The
crucial point
is that for sufficiently small displacements the Earth's surface is approximately planar, and
vector displacements on a plane surface commute with one another. This observation immediately
suggests that rotation ``vectors'' which correspond to rotations through small angles
must also commute with
one another. In other words, although the quantity
northwards,
we end up at the North pole. Hence, large rotations over the Earth's surface do
not commute.
Let us now repeat this experiment on a far smaller
scale. Suppose that we walk 10m northwards and then 10m eastwards.
Next, suppose that--starting from
the same initial position--we walk 10m eastwards and then 10m northwards. In this case, few people
would need much convincing that the two end points are essentially identical. The
crucial point
is that for sufficiently small displacements the Earth's surface is approximately planar, and
vector displacements on a plane surface commute with one another. This observation immediately
suggests that rotation ``vectors'' which correspond to rotations through small angles
must also commute with
one another. In other words, although the quantity
![]() , defined above, is not a true
vector, the infinitesimal quantity
, defined above, is not a true
vector, the infinitesimal quantity
![]() , which is defined in a similar manner but
corresponds to a rotation through an infinitesimal angle
, which is defined in a similar manner but
corresponds to a rotation through an infinitesimal angle ![]() , is a perfectly good
vector.
, is a perfectly good
vector.
![]() which
describes a rotation through a small angle
which
describes a rotation through a small angle ![]() about a fixed axis. But, how is this
definition
useful? Well, suppose that vector
about a fixed axis. But, how is this
definition
useful? Well, suppose that vector
![]() describes the small rotation that a given
object executes in the infinitesimal time interval between
describes the small rotation that a given
object executes in the infinitesimal time interval between ![]() and
and ![]() . We can
then define the quantity
. We can
then define the quantity
![]() .
Let us now combine this motion with rotation about a different axis at constant
angular velocity
.
Let us now combine this motion with rotation about a different axis at constant
angular velocity
![]() . What is the subsequent motion of the body? Since we know
that angular velocity is a vector, we can be certain that the combined motion simply
corresponds to rotation about a third axis at constant angular velocity
. What is the subsequent motion of the body? Since we know
that angular velocity is a vector, we can be certain that the combined motion simply
corresponds to rotation about a third axis at constant angular velocity