


Next: Is rotation a vector?
Up: Rotational motion
Previous: Introduction
Consider a rigid body executing pure rotational motion (i.e., rotational motion which
has no translational component). It is possible to define an axis of rotation
(which, for the sake of simplicity, is assumed to pass through the body)--this
axis corresponds to the straight-line
which is the locus of all points inside the body which remain stationary as the body rotates. A general point
located inside the body executes circular motion which is centred on the rotation axis, and orientated
in the plane perpendicular to this axis. In the following, we tacitly assume that the axis
of rotation remains fixed.
Figure 67:
Rigid body rotation.
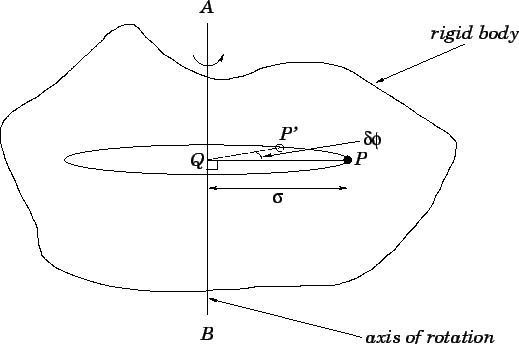 |
Figure 67 shows a typical rigidly
rotating body. The axis of rotation is the line 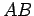 . A general point
. A general point
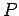 lying within the body executes a circular orbit, centred on
lying within the body executes a circular orbit, centred on 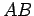 , in the plane perpendicular to
, in the plane perpendicular to
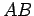 . Let the line
. Let the line 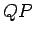 be a radius of this orbit which links the axis of rotation to the
instantaneous position of
be a radius of this orbit which links the axis of rotation to the
instantaneous position of 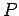 at time
at time  . Obviously, this implies that
. Obviously, this implies that 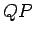 is normal
to
is normal
to 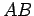 . Suppose that at time
. Suppose that at time 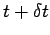 point
point 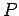 has moved to
has moved to 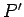 , and the radius
, and the radius
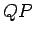 has rotated through an angle
has rotated through an angle 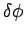 . The instantaneous
angular velocity of the body
. The instantaneous
angular velocity of the body 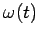 is defined
is defined
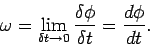 |
(309) |
Note that if the body is indeed rotating rigidly, then the calculated value of  should
be the same for all possible points
should
be the same for all possible points 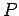 lying within the body (except for those points lying
exactly on the axis of rotation, for which
lying within the body (except for those points lying
exactly on the axis of rotation, for which  is ill-defined).
The rotation speed
is ill-defined).
The rotation speed  of point
of point 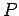 is related to the angular velocity
is related to the angular velocity  of the body via
of the body via
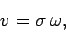 |
(310) |
where 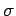 is the perpendicular distance from the axis of rotation to
point
is the perpendicular distance from the axis of rotation to
point 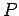 . Thus,
in a rigidly rotating body, the rotation speed increases linearly with (perpendicular) distance
from the axis of rotation.
. Thus,
in a rigidly rotating body, the rotation speed increases linearly with (perpendicular) distance
from the axis of rotation.
It is helpful to introduce the angular acceleration  of a rigidly rotating body:
this quantity is defined as the
time derivative of the angular velocity. Thus,
of a rigidly rotating body:
this quantity is defined as the
time derivative of the angular velocity. Thus,
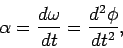 |
(311) |
where 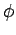 is the angular coordinate of some arbitrarily chosen point reference
within the body, measured
with respect to the rotation axis.
Note that angular velocities are conventionally measured in radians per second, whereas angular
accelerations are measured in radians per second squared.
is the angular coordinate of some arbitrarily chosen point reference
within the body, measured
with respect to the rotation axis.
Note that angular velocities are conventionally measured in radians per second, whereas angular
accelerations are measured in radians per second squared.
For a body rotating with constant angular velocity,  ,
the angular acceleration is zero, and the rotation angle
,
the angular acceleration is zero, and the rotation angle 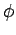 increases linearly with time:
increases linearly with time:
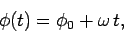 |
(312) |
where
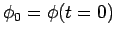 . Likewise, for a body rotating with constant angular acceleration,
. Likewise, for a body rotating with constant angular acceleration,
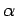 , the angular velocity increases linearly with time, so that
, the angular velocity increases linearly with time, so that
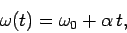 |
(313) |
and the rotation angle satisfies
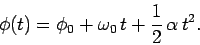 |
(314) |
Here,
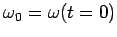 . Note that there is a clear analogy between the above
equations, and the equations of rectilinear motion at constant acceleration introduced in
Sect. 2.6--rotation angle plays the role of displacement, angular velocity plays the role of (regular) velocity, and
angular acceleration plays the role of (regular) acceleration.
. Note that there is a clear analogy between the above
equations, and the equations of rectilinear motion at constant acceleration introduced in
Sect. 2.6--rotation angle plays the role of displacement, angular velocity plays the role of (regular) velocity, and
angular acceleration plays the role of (regular) acceleration.



Next: Is rotation a vector?
Up: Rotational motion
Previous: Introduction
Richard Fitzpatrick
2006-02-02

![]() . A general point
. A general point
![]() lying within the body executes a circular orbit, centred on
lying within the body executes a circular orbit, centred on ![]() , in the plane perpendicular to
, in the plane perpendicular to
![]() . Let the line
. Let the line ![]() be a radius of this orbit which links the axis of rotation to the
instantaneous position of
be a radius of this orbit which links the axis of rotation to the
instantaneous position of ![]() at time
at time ![]() . Obviously, this implies that
. Obviously, this implies that ![]() is normal
to
is normal
to ![]() . Suppose that at time
. Suppose that at time ![]() point
point ![]() has moved to
has moved to ![]() , and the radius
, and the radius
![]() has rotated through an angle
has rotated through an angle ![]() . The instantaneous
angular velocity of the body
. The instantaneous
angular velocity of the body ![]() is defined
is defined
![]() of a rigidly rotating body:
this quantity is defined as the
time derivative of the angular velocity. Thus,
of a rigidly rotating body:
this quantity is defined as the
time derivative of the angular velocity. Thus,
![]() ,
the angular acceleration is zero, and the rotation angle
,
the angular acceleration is zero, and the rotation angle ![]() increases linearly with time:
increases linearly with time: