


Next: Worked example 5.1: Bucket
Up: Conservation of energy
Previous: Motion in a general
Power
Suppose that an object moves in a general force-field
 .
We now know how to calculate how much energy flows from the force-field
to the object as it moves along a given path between two
points. Let us now consider the rate at which this energy flows.
If
.
We now know how to calculate how much energy flows from the force-field
to the object as it moves along a given path between two
points. Let us now consider the rate at which this energy flows.
If 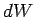 is the amount of work that the force-field performs on the mass
in a time interval
is the amount of work that the force-field performs on the mass
in a time interval 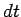 then the rate of working is given by
then the rate of working is given by
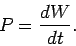 |
(176) |
In other words, the rate of working--which is usually referred to as the
power--is simply the time derivative of the work performed.
Incidentally, the mks unit of power is called the watt (symbol W). In
fact, 1 watt equals 1 kilogram meter-squared per second-cubed, or
1 joule per second.
Suppose that the object displaces by 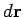 in the time interval
in the time interval
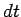 . By definition, the amount of work done on the object
during this time interval is given by
. By definition, the amount of work done on the object
during this time interval is given by
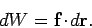 |
(177) |
It follows from Eq. (176) that
 |
(178) |
where
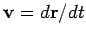 is the object's instantaneous velocity.
Note that power can be positive or negative, depending on the relative
directions of the vectors
is the object's instantaneous velocity.
Note that power can be positive or negative, depending on the relative
directions of the vectors 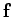 and
and 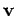 . If these
two vectors are mutually perpendicular then the power is zero.
For the case of 1-dimensional motion, the above expression reduces to
. If these
two vectors are mutually perpendicular then the power is zero.
For the case of 1-dimensional motion, the above expression reduces to
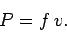 |
(179) |
In other words, in 1-dimension, power simply equals force times velocity.



Next: Worked example 5.1: Bucket
Up: Conservation of energy
Previous: Motion in a general
Richard Fitzpatrick
2006-02-02
![]() in the time interval
in the time interval
![]() . By definition, the amount of work done on the object
during this time interval is given by
. By definition, the amount of work done on the object
during this time interval is given by