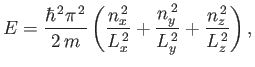
where
- Suppose that the particle is in a given state specified by
particular values of the three quantum numbers,
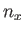 ,
, 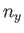 ,
, 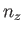 . By
considering how the energy of this state must change when the length,
. By
considering how the energy of this state must change when the length, 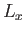 , of
the box parallel to the
, of
the box parallel to the 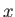 -axis is very slowly changed by a small amount
-axis is very slowly changed by a small amount 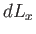 , show that the force exerted
by a particle in this state on a wall perpendicular to the
, show that the force exerted
by a particle in this state on a wall perpendicular to the 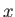 -axis is given
by
-axis is given
by
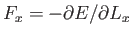 .
.
- Explicitly calculate the force per unit area (or pressure) acting on this wall.
By averaging over all possible states, find an expression for the mean pressure
on this wall. (Hint: exploit the fact that
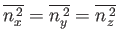 must all be equal, by symmetry.) Show that this mean pressure can be
written
must all be equal, by symmetry.) Show that this mean pressure can be
written
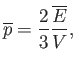
where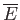 is the mean energy of the particle,
and
is the mean energy of the particle,
and
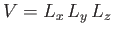 the volume of the box.
the volume of the box.
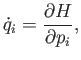
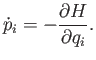
Here,
- Show that
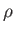 evolves in time according to Liouville's theorem:
evolves in time according to Liouville's theorem:
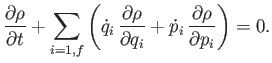
[Hint: Consider how the the flux of systems into a small volume of phase-space causes the number of systems in the volume to change in time.] - By definition,
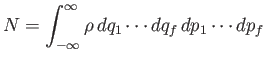
is the total number of systems in the ensemble. The integral is over all of phase-space. Show that Liouville's theorem conserves the total number of systems (i.e.,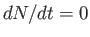 ). You may assume that
). You may assume that 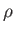 becomes negligibly
small if any of its arguments (i.e.,
becomes negligibly
small if any of its arguments (i.e.,
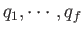 and
and
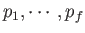 ) becomes very large. This is equivalent to assuming that
all of the systems are localized to some region of phase-space.
) becomes very large. This is equivalent to assuming that
all of the systems are localized to some region of phase-space.
- Suppose that
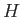 has no explicit time dependence
(i.e.,
has no explicit time dependence
(i.e.,
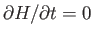 ).
Show that the ensemble-averaged energy,
).
Show that the ensemble-averaged energy,
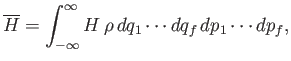
is a constant of the motion. - Show that if
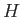 is also not an explicit function of the coordinate
is also not an explicit function of the coordinate 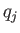 then the ensemble average of the conjugate momentum,
then the ensemble average of the conjugate momentum,
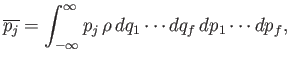
is a constant of the motion.
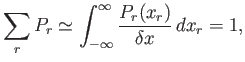
where the summation is over all possible values. Suppose that we know the mean and the variance of
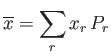
and
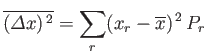
are both fixed. According to the
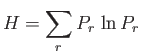
is minimized. Used the method of Lagrange multipliers to minimixe
![$\displaystyle P_r (x_r)\simeq \frac{\delta x}{ \sqrt{2\pi \overline{({\mit \De...
...\frac{(x_r-\overline{x})^{ 2}}{2 \overline{({\mit \Delta} x)^{ 2}}}\right].
$](img453.png)
This result demonstrates that the system will naturally evolve towards a final equilibrium state in which all of its macroscopic variables have Gaussian probability distributions, which is in accordance with the central limit theorem. (See Section 2.10.)