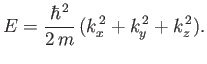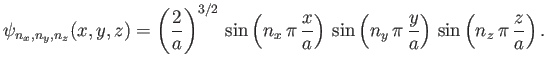Next: Simple Harmonic Oscillator
Up: Wave Mechanics
Previous: Stationary States
Three-Dimensional Wave Mechanics
Up to now, we have only discussed wave mechanics for a particle moving in one dimension. However, the
generalization to a particle moving in three dimensions is fairly straightforward.
A massive particle moving in three dimensions
has a complex wavefunction of the form [cf., Equation (C.15)]
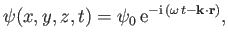 |
(C.80) |
where 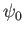 is a complex constant, and
is a complex constant, and
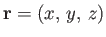 . Here, the wavevector,
. Here, the wavevector, 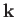 , and
the angular frequency,
, and
the angular frequency,  , are related to the particle momentum,
, are related to the particle momentum, 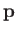 , and energy,
, and energy,  , according
to [cf., Equations (C.3) and (C.27)]
, according
to [cf., Equations (C.3) and (C.27)]
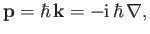 |
(C.81) |
and [cf., Equation (C.1)]
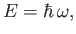 |
(C.82) |
respectively. Generalizing the
analysis of Section C.5, the three-dimensional version of Schrödinger's
equation is [cf., Equations (C.24) and (C.29)]
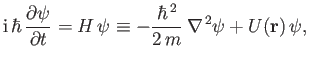 |
(C.83) |
where
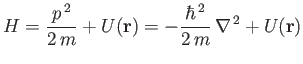 |
(C.84) |
is the Hamiltonian, and the differential operator
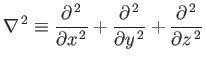 |
(C.85) |
is known as the Laplacian. The interpretation of a three-dimensional wavefunction is that the
probability of simultaneously finding the particle between  and
and 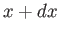 , between
, between  and
and 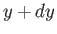 , and
between
, and
between 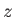 and
and 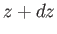 , at time
, at time  is [cf., Equation (C.30)]
is [cf., Equation (C.30)]
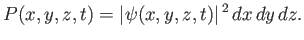 |
(C.86) |
Moreover, the normalization condition for the wavefunction becomes [cf., Equation (C.32)]
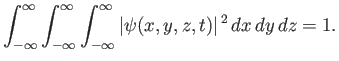 |
(C.87) |
It can be demonstrated that Schrödinger's equation, (C.83), preserves the normalization
condition, (C.87), of a localized wavefunction.
Heisenberg's uncertainty principle generalizes to [cf., Equation (C.60)]
Finally, a stationary state of energy  is written [cf., Equation (C.64)]
is written [cf., Equation (C.64)]
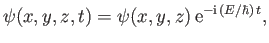 |
(C.91) |
where the stationary wavefunction,
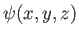 , satisfies [cf., Equation (C.66)]
, satisfies [cf., Equation (C.66)]
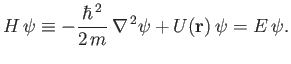 |
(C.92) |
As an example of a three-dimensional problem in wave mechanics, consider a particle trapped in a square potential well of infinite depth,
such that
![$\displaystyle U(x,y,z) = \left\{ \begin{array}{lll} 0&\mbox{\hspace{0.5cm}}&0\l...
...\leq a, 0\leq z\leq a\ [0.5ex] \infty &&\mbox{otherwise} \end{array}\right..$](img3246.png) |
(C.93) |
Within the well, the stationary wavefunction,
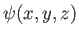 , satisfies
, satisfies
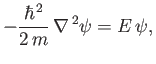 |
(C.94) |
subject to the boundary conditions
 |
(C.95) |
and
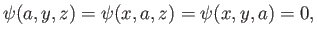 |
(C.96) |
because 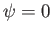 outside the well.
Let us try a separable wavefunction of the form
outside the well.
Let us try a separable wavefunction of the form
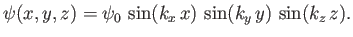 |
(C.97) |
This expression automatically satisfies the boundary conditions (C.95). The
remaining boundary conditions, (C.96), are satisfied provided
where the quantum numbers 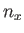 ,
, 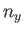 , and
, and 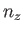 are (independent) positive integers. Note that a stationary state generally possesses as many
quantum numbers as there are degrees of freedom of the system (in this case, three).
Substitution of the wavefunction (C.97) into Equation (C.94)
yields
are (independent) positive integers. Note that a stationary state generally possesses as many
quantum numbers as there are degrees of freedom of the system (in this case, three).
Substitution of the wavefunction (C.97) into Equation (C.94)
yields
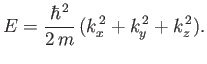 |
(C.101) |
Thus, it follows from Equations (C.98)-(C.100) that the particle energy is quantized, and that the
allowed energy levels are
 |
(C.102) |
The properly normalized [see Equation (C.87)] stationary wavefunctions corresponding to
these energy levels are
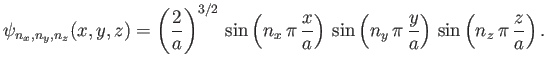 |
(C.103) |
As is the case for a particle trapped in a one-dimensional potential well, the lowest
energy level for a particle trapped in a three-dimensional well is not zero, but rather
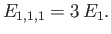 |
(C.104) |
Here,
 |
(C.105) |
is the ground state (i.e., the lowest energy state) energy in the one-dimensional
case.
It follows from Equation (C.102) that distinct permutations of 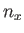 ,
, 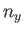 , and
, and 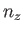 that do
not alter the value of
that do
not alter the value of
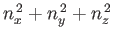 also do not alter the energy. In other words, in three dimensions,
it is possible for distinct wavefunctions to be associated with the same energy level. In this
situation, the energy level is said to be degenerate. The ground state energy level,
also do not alter the energy. In other words, in three dimensions,
it is possible for distinct wavefunctions to be associated with the same energy level. In this
situation, the energy level is said to be degenerate. The ground state energy level, 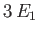 , is non-degenerate,
because the only combination of (
, is non-degenerate,
because the only combination of (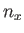 ,
, 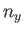 ,
, 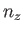 ) that gives this energy is (
) that gives this energy is (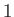 ,
, 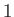 ,
, 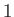 ).
However, the next highest energy level,
).
However, the next highest energy level, 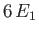 , is degenerate, because it is obtained when (
, is degenerate, because it is obtained when (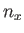 ,
, 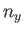 ,
, 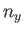 )
take the values (
)
take the values (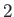 ,
, 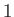 ,
, 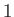 ),
or (
),
or (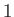 ,
, 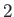 ,
, 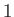 ), or (
), or (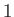 ,
, 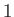 ,
, 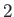 ). In fact, a non-degenerate energy
level corresponds to a case where the three quantum numbers (i.e.,
). In fact, a non-degenerate energy
level corresponds to a case where the three quantum numbers (i.e., 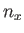 ,
, 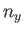 , and
, and 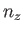 ) all have
the same value, whereas a three-fold degenerate energy level corresponds to a case where only
two of the quantum numbers have the same value, and, finally, a six-fold degenerate energy level corresponds to a
case where the quantum numbers are all different.
) all have
the same value, whereas a three-fold degenerate energy level corresponds to a case where only
two of the quantum numbers have the same value, and, finally, a six-fold degenerate energy level corresponds to a
case where the quantum numbers are all different.



Next: Simple Harmonic Oscillator
Up: Wave Mechanics
Previous: Stationary States
Richard Fitzpatrick
2016-01-25
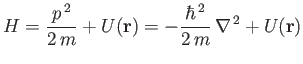
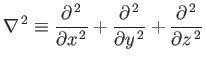
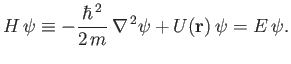
![$\displaystyle U(x,y,z) = \left\{ \begin{array}{lll} 0&\mbox{\hspace{0.5cm}}&0\l...
...\leq a, 0\leq z\leq a\ [0.5ex] \infty &&\mbox{otherwise} \end{array}\right..$](img3246.png)