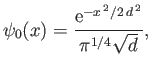Next: Angular Momentum
Up: Wave Mechanics
Previous: Three-Dimensional Wave Mechanics
Simple Harmonic Oscillator
The classical Hamiltonian of a simple harmonic oscillator is
 |
(C.106) |
where 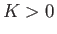 is the so-called force constant of the oscillator. Assuming that the quantum-mechanical Hamiltonian has the same form as the classical Hamiltonian, the time-independent Schrödinger equation for a particle of mass
is the so-called force constant of the oscillator. Assuming that the quantum-mechanical Hamiltonian has the same form as the classical Hamiltonian, the time-independent Schrödinger equation for a particle of mass  and energy
and energy  moving in a
simple harmonic potential becomes
moving in a
simple harmonic potential becomes
 |
(C.107) |
Let
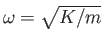 , where
, where  is the oscillator's classical angular frequency of oscillation. Furthermore, let
is the oscillator's classical angular frequency of oscillation. Furthermore, let
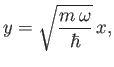 |
(C.108) |
and
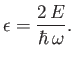 |
(C.109) |
Equation (C.107) reduces to
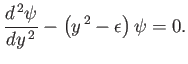 |
(C.110) |
We need to find solutions to the previous equation that are bounded
at infinity. In other words, solutions that satisfy the boundary
condition
 as
as
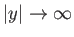 .
.
Consider the behavior of the solution to Equation (C.110) in the limit 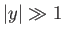 . As is easily seen, in this limit, the equation simplifies somewhat to give
. As is easily seen, in this limit, the equation simplifies somewhat to give
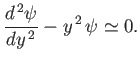 |
(C.111) |
The approximate solutions to the previous equation are
 |
(C.112) |
where 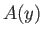 is a relatively slowly-varying function of
is a relatively slowly-varying function of  .
Clearly, if
.
Clearly, if 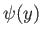 is to remain bounded as
is to remain bounded as
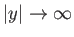 then we
must chose the exponentially decaying solution. This suggests that
we should write
then we
must chose the exponentially decaying solution. This suggests that
we should write
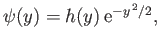 |
(C.113) |
where we would expect 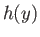 to be an algebraic, rather than an exponential, function of
to be an algebraic, rather than an exponential, function of  .
.
Substituting Equation (C.113) into Equation (C.110), we obtain
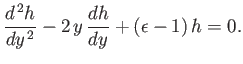 |
(C.114) |
Let us attempt a power-law solution of the form
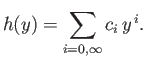 |
(C.115) |
Inserting this test solution into Equation (C.114), and equating the
coefficients of 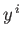 , we obtain the recursion relation
, we obtain the recursion relation
 |
(C.116) |
Consider the behavior of 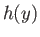 in the limit
in the limit
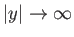 .
The previous recursion relation simplifies to
.
The previous recursion relation simplifies to
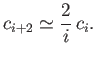 |
(C.117) |
Hence, at large  , when the higher powers of
, when the higher powers of  dominate, we
have
dominate, we
have
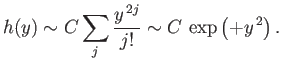 |
(C.118) |
It follows that
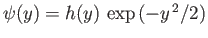 varies as
varies as
 as
as
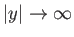 . This behavior is unacceptable,
because it does not satisfy the boundary condition
. This behavior is unacceptable,
because it does not satisfy the boundary condition
 as
as
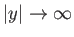 . The only way in which we can prevent
. The only way in which we can prevent 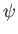 from blowing up as
from blowing up as
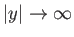 is to demand that the power series (C.115) terminate at
some finite value of
is to demand that the power series (C.115) terminate at
some finite value of  . This implies, from the recursion relation
(C.116), that
. This implies, from the recursion relation
(C.116), that
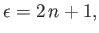 |
(C.119) |
where  is a non-negative integer. Note that the number of terms in the power
series (C.115) is
is a non-negative integer. Note that the number of terms in the power
series (C.115) is 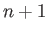 . Finally, using Equation (C.109), we obtain
. Finally, using Equation (C.109), we obtain
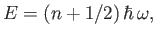 |
(C.120) |
for
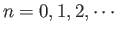 .
.
Hence, we conclude that a particle moving in a
harmonic potential has quantized energy levels that
are equally spaced. The
spacing between successive energy levels is
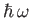 , where
, where
 is the classical oscillation frequency. Furthermore, the
lowest energy state (
is the classical oscillation frequency. Furthermore, the
lowest energy state ( ) possesses the finite energy
) possesses the finite energy
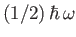 . This is sometimes called zero-point energy.
It is easily demonstrated that the (normalized) wavefunction of the lowest-energy state takes the form
. This is sometimes called zero-point energy.
It is easily demonstrated that the (normalized) wavefunction of the lowest-energy state takes the form
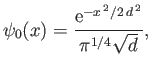 |
(C.121) |
where
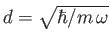 .
.



Next: Angular Momentum
Up: Wave Mechanics
Previous: Three-Dimensional Wave Mechanics
Richard Fitzpatrick
2016-01-25


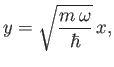
![]() . As is easily seen, in this limit, the equation simplifies somewhat to give
. As is easily seen, in this limit, the equation simplifies somewhat to give
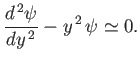
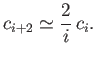
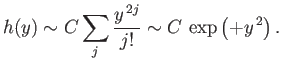
![]() , where
, where
![]() is the classical oscillation frequency. Furthermore, the
lowest energy state (
is the classical oscillation frequency. Furthermore, the
lowest energy state (![]() ) possesses the finite energy
) possesses the finite energy
![]() . This is sometimes called zero-point energy.
It is easily demonstrated that the (normalized) wavefunction of the lowest-energy state takes the form
. This is sometimes called zero-point energy.
It is easily demonstrated that the (normalized) wavefunction of the lowest-energy state takes the form