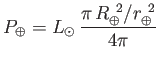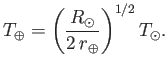Next: Conduction Electrons in Metal
Up: Quantum Statistics
Previous: Black-Body Radiation
The total power radiated per unit area by a black-body at all
frequencies is given by
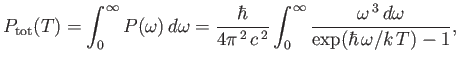 |
(8.125) |
or
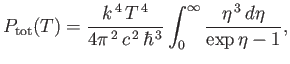 |
(8.126) |
where
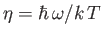 . The previous integral can easily be looked up in
standard mathematical tables. In fact,
. The previous integral can easily be looked up in
standard mathematical tables. In fact,
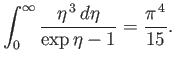 |
(8.127) |
(See Exercise 2.)
Thus, the total power radiated per unit area by a black-body is
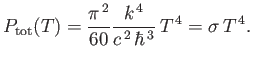 |
(8.128) |
This 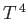 dependence of the radiated power is called the Stefan-Boltzmann law,
after Josef Stefan, who first obtained it
experimentally, and Ludwig Boltzmann, who first derived it theoretically.
The parameter
dependence of the radiated power is called the Stefan-Boltzmann law,
after Josef Stefan, who first obtained it
experimentally, and Ludwig Boltzmann, who first derived it theoretically.
The parameter
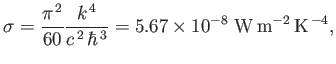 |
(8.129) |
is called the Stefan-Boltzmann constant.
We can use the Stefan-Boltzmann law to estimate the temperature of the Earth
from first principles. The Sun is a ball of glowing gas of radius
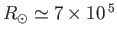 km and surface temperature
km and surface temperature
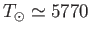 K. Its
luminosity is
K. Its
luminosity is
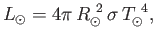 |
(8.130) |
according to the Stefan-Boltzmann law. The Earth is a globe of radius
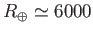 km located an average distance
km located an average distance
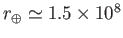 km
from the Sun. The Earth intercepts an amount of energy
km
from the Sun. The Earth intercepts an amount of energy
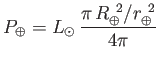 |
(8.131) |
per second from the Sun's radiative output: that is, the power output of the Sun
reduced by the ratio of the solid angle subtended by the Earth at the Sun to
the total solid angle 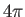 . The Earth absorbs this energy, and then
re-radiates it at longer wavelengths. The luminosity of the Earth is
. The Earth absorbs this energy, and then
re-radiates it at longer wavelengths. The luminosity of the Earth is
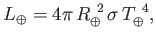 |
(8.132) |
according to the Stefan-Boltzmann law,
where 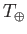 is the average temperature of the Earth's surface.
Here, we are ignoring
any surface
temperature variations between polar and equatorial regions, or between day
and night. In steady-state, the luminosity of the Earth must balance the radiative
power input from the Sun,
so equating
is the average temperature of the Earth's surface.
Here, we are ignoring
any surface
temperature variations between polar and equatorial regions, or between day
and night. In steady-state, the luminosity of the Earth must balance the radiative
power input from the Sun,
so equating 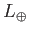 and
and 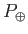 we arrive at
we arrive at
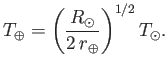 |
(8.133) |
Remarkably, the ratio of the Earth's surface temperature to that of the Sun depends
only on the Earth-Sun distance and the solar radius. The previous expression
yields
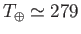 K or
K or 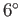 C (or
C (or 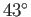 F). This is slightly on the cold side, by a few
degrees, because of the
greenhouse action of the Earth's atmosphere,
which was neglected in our
calculation. Nevertheless, it is quite encouraging that such a crude calculation
comes so close to the correct answer.
F). This is slightly on the cold side, by a few
degrees, because of the
greenhouse action of the Earth's atmosphere,
which was neglected in our
calculation. Nevertheless, it is quite encouraging that such a crude calculation
comes so close to the correct answer.



Next: Conduction Electrons in Metal
Up: Quantum Statistics
Previous: Black-Body Radiation
Richard Fitzpatrick
2016-01-25
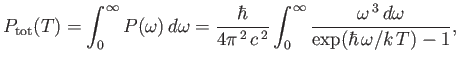
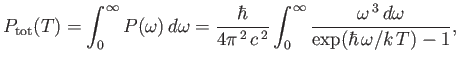
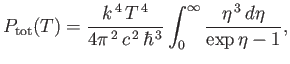
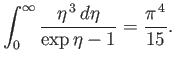
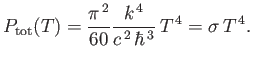
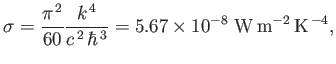
![]() km and surface temperature
km and surface temperature
![]() K. Its
luminosity is
K. Its
luminosity is