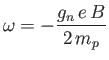Next: Pauli Two-Component Formalism
Up: Spin Angular Momentum
Previous: Magnetic Moments
Spin Precession
The Hamiltonian for an electron at rest in a  -directed magnetic field,
-directed magnetic field,
 ,
is [49]
,
is [49]
where
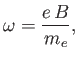 |
(5.49) |
and use has been made of Equation (5.47).
According to Equation (3.28), the time evolution operator for this system is
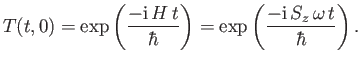 |
(5.50) |
It can be seen, by comparison with Equation (5.24), that the time evolution operator
is precisely the same as the rotation (about the  -axis) operator for spin, with
-axis) operator for spin, with
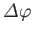 set
equal to
set
equal to
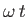 . It is immediately clear that the Hamiltonian (5.48)
causes the electron
spin to precess about the
. It is immediately clear that the Hamiltonian (5.48)
causes the electron
spin to precess about the  -axis with angular frequency
-axis with angular frequency 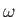 . In fact,
Equations (5.35)-(5.37) imply that
. In fact,
Equations (5.35)-(5.37) imply that
Note that the expectation value of the electron spin precesses in a right-handed fashion. In other words, if the thumb of the right
hand is directed along the magnetic field then the fingers of the right-hand indicate the direction of the precession.
A particle with a positive  -factor would precess in a left-handed fashion.
The time evolution of the state ket is given by analogy with Equation (5.40):
-factor would precess in a left-handed fashion.
The time evolution of the state ket is given by analogy with Equation (5.40):
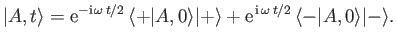 |
(5.54) |
Note that it takes a time
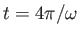 for the state ket to return to its
original state.
By contrast, it only takes a time
for the state ket to return to its
original state.
By contrast, it only takes a time
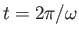 for the spin vector to point
in its original direction.
for the spin vector to point
in its original direction.
We shall now describe an experiment to detect the minus sign in Equation (5.41). An almost
mono-energetic beam of neutrons is split in two, sent along two different
paths, I and II, and then recombined. Path I passes through a
magnetic-field-free region. However, path II enters a small region where a static magnetic
field is present. As a result, a neutron state ket going along path
II acquires a phase-shift
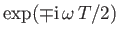 (the
(the  signs correspond to
signs correspond to
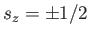 states). Here,
states). Here, 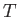 is the
time spent in the magnetic field, and
is the
time spent in the magnetic field, and
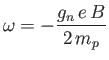 |
(5.55) |
is the spin precession frequency.
Moreover, 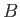 is the magnetic field-strength,
is the magnetic field-strength, 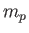 the proton mass, and
the proton mass, and  the neutron
the neutron  -factor. This factor is found experimentally to take the value
-factor. This factor is found experimentally to take the value
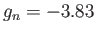 [60].
(The magnetic moment of a neutron is entirely a quantum field effect. Incidentally, this particular experiment must be
performed with electrically neutral particles because, otherwise, the particles that pass through the magnetic
field would be strongly perturbed by the Lorentz force.)
When neutrons from path I and path II meet they undergo interference. We
expect the observed neutron intensity in the interference region to
exhibit a
[60].
(The magnetic moment of a neutron is entirely a quantum field effect. Incidentally, this particular experiment must be
performed with electrically neutral particles because, otherwise, the particles that pass through the magnetic
field would be strongly perturbed by the Lorentz force.)
When neutrons from path I and path II meet they undergo interference. We
expect the observed neutron intensity in the interference region to
exhibit a
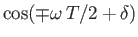 variation,
where
variation,
where 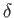 is the phase difference
between paths I and II in the absence of a magnetic field. In experiments,
the time of flight
is the phase difference
between paths I and II in the absence of a magnetic field. In experiments,
the time of flight 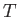 through the magnetic field region is kept constant, while
the field-strength
through the magnetic field region is kept constant, while
the field-strength 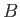 is varied. It follows that the change in magnetic
field required to produce successive maxima is
is varied. It follows that the change in magnetic
field required to produce successive maxima is
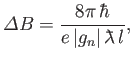 |
(5.56) |
where  is the path-length through the magnetic field region, and
is the path-length through the magnetic field region, and
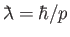 is the reduced (by a factor
is the reduced (by a factor 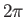 ) de Broglie wavelength of the neutrons. The previous formula has been verified
experimentally to within a fraction of a percent [89,116]. Note that the formula in question depends crucially
on the fact that it takes a
) de Broglie wavelength of the neutrons. The previous formula has been verified
experimentally to within a fraction of a percent [89,116]. Note that the formula in question depends crucially
on the fact that it takes a 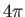 rotation to return a state ket to its
original state. If it only took a
rotation to return a state ket to its
original state. If it only took a 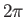 rotation then
rotation then
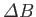 would take half
of the value given in Equation (5.56), which does not agree with the experimental data.
would take half
of the value given in Equation (5.56), which does not agree with the experimental data.



Next: Pauli Two-Component Formalism
Up: Spin Angular Momentum
Previous: Magnetic Moments
Richard Fitzpatrick
2016-01-22

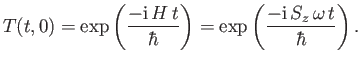
![]() (the
(the ![]() signs correspond to
signs correspond to
![]() states). Here,
states). Here, ![]() is the
time spent in the magnetic field, and
is the
time spent in the magnetic field, and