Next: Bibliography Up: Plasma Fluid Theory Previous: Normalization of Neoclassical Fluid Contents
In this book, however, we intend to use the neoclassical fluid equations, (2.370)–(2.374), to describe the evolution of a tokamak plasma equilibrium that is perturbed by a non-axisymmetric tearing mode. This
approach requires some justification. The first justification is that tearing modes in tokamak plasmas usually saturate at a fairly low amplitudes (typically
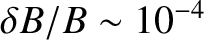 ) [52]. Hence, the departure from axisymmetry associated with the tearing modes is
comparatively small. The second justification is that
tearing modes do not affect the plasma collisionality, and, in particular, do not significantly modify particle trapping. The third justification is that tearing modes are sufficiently
slowly growing that they do not give rise to perturbed E-cross-B flows that are large enough to violate the drift ordering [28,29]. It is harder to argue
that tearing modes are sufficiently slowly growing that they do not violate the transport ordering. It is certainly the
case that large amplitude tearing modes grow on timescales that are comparable to a transport timescale (because
such modes are effectively slightly-helical plasma equilibria) [45]. However, low amplitude tearing modes can grow on somewhat shorter timescales [21]. Furthermore, diamagnetic effects cause tearing modes to
propagate with respect to the MHD fluid [2], which is the origin of the modified ordering (2.362). We are essentially hoping that this slightly faster time evolution does not invalidate our analysis. The final justification is that, to a first approximation, tearing modes do not modify, and are not
directly affected by, plasma turbulence. Of course, this is not strictly true,
because a sufficiently large amplitude tearing mode can flatten the density and pressure profiles, and, thereby, stabilize micro-instabilities—which has the effect of reducing turbulent transport—in the immediate vicinity of its
rational surface [12,3,4,35]. Under certain circumstance, turbulence can also directly influence tearing mode
evolution [12,13,46]. Unfortunately, the mutual interaction between plasma turbulence and a tearing mode is almost impossible to model accurately with fluid equations, and will, therefore, be neglected in this book.
) [52]. Hence, the departure from axisymmetry associated with the tearing modes is
comparatively small. The second justification is that
tearing modes do not affect the plasma collisionality, and, in particular, do not significantly modify particle trapping. The third justification is that tearing modes are sufficiently
slowly growing that they do not give rise to perturbed E-cross-B flows that are large enough to violate the drift ordering [28,29]. It is harder to argue
that tearing modes are sufficiently slowly growing that they do not violate the transport ordering. It is certainly the
case that large amplitude tearing modes grow on timescales that are comparable to a transport timescale (because
such modes are effectively slightly-helical plasma equilibria) [45]. However, low amplitude tearing modes can grow on somewhat shorter timescales [21]. Furthermore, diamagnetic effects cause tearing modes to
propagate with respect to the MHD fluid [2], which is the origin of the modified ordering (2.362). We are essentially hoping that this slightly faster time evolution does not invalidate our analysis. The final justification is that, to a first approximation, tearing modes do not modify, and are not
directly affected by, plasma turbulence. Of course, this is not strictly true,
because a sufficiently large amplitude tearing mode can flatten the density and pressure profiles, and, thereby, stabilize micro-instabilities—which has the effect of reducing turbulent transport—in the immediate vicinity of its
rational surface [12,3,4,35]. Under certain circumstance, turbulence can also directly influence tearing mode
evolution [12,13,46]. Unfortunately, the mutual interaction between plasma turbulence and a tearing mode is almost impossible to model accurately with fluid equations, and will, therefore, be neglected in this book.
As we saw in the previous section, under normal circumstances the neoclassical fluid equations, (2.370)–(2.374), reduce to
the much simpler equations of marginally-stable ideal-MHD, (2.375)–(2.380). However, as we shall demonstrate in the next chapter, when applied to tearing mode dynamics, the equations of marginally-stable ideal-MHD become singular at the associated rational magnetic flux-surface. (See Section 3.7.) The singularity
is resolved in a thin current sheet characterized by
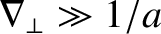 and
and
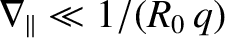 . [See
Equations (2.352) and (2.353).] When we reorder the neoclassical
fluid equations, using appropriate estimates for
. [See
Equations (2.352) and (2.353).] When we reorder the neoclassical
fluid equations, using appropriate estimates for
 and
and
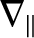 within the layer, we shall discover that most of the terms in the equations need to be retained.
within the layer, we shall discover that most of the terms in the equations need to be retained.