Plasma Species

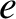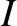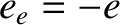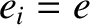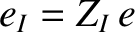The plasma is assumed to consist of three (charged) species; namely, electrons ($e$), majority ions ($i$), and impurity ions ($I$). The charges of the three species are $e_e=-e$, $e_i= e$, and $e_I=Z_I\,e$, respectively, where 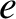$e$ is the magnitude of the electron charge. Quasi-neutrality [1] demands that

$$n_e= n_i+ Z_I\,n_I,$$ (A.1)

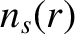where $n_s(r)$ is the species-$s$ number density. Here, $r$ is the flux-surface label introduced in Section 14.2. Let

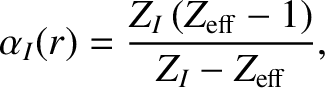$$\alpha_I(r) =\frac{Z_I\,(Z_{\rm eff}-1)}{Z_I-Z_{\rm eff}},$$ (A.2)

where

$$Z_{\rm eff}(r) = \frac{n_i+Z_I^{\,2}\,n_I}{n_e}$$ (A.3)

is the effective ion charge number. (See Section 1.6.) It follows that

$$\frac{n_i}{n_e} = \frac{Z_I-Z_{\rm eff}}{Z_I-1},$$ (A.4)

$$\frac{n_I}{n_e} = \frac{Z_{\rm eff}-1}{Z_I\,(Z_I-1)}.$$ (A.5)

Finally, let

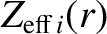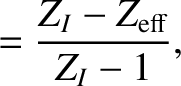$$Z_{{\rm eff}\,i}(r) = \frac{Z_I-Z_{\rm eff}}{Z_I-1},$$ (A.6)

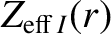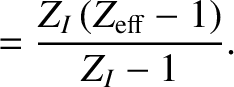$$Z_{{\rm eff}\,I}(r) =\frac{Z_I\,(Z_{\rm eff}-1)}{Z_I-1}.$$ (A.7)

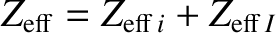Note that $Z_{\rm eff} = Z_{{\rm eff}\,i}+Z_{{\rm eff}\,I}$.