


Next: Solar Wind
Up: Magnetohydrodynamic Fluids
Previous: Flux Freezing
MHD Waves
Let us investigate the small amplitude waves that propagate through
a spatially uniform MHD plasma. We start by combining Equations (7.1)-(7.4) and (7.7)-(7.8) to form a
closed set of equations:
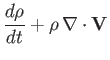 |
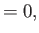 |
(7.22) |
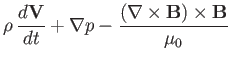 |
 |
(7.23) |
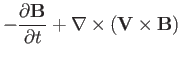 |
 |
(7.24) |
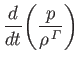 |
 |
(7.25) |
Next, we linearize these equations (assuming, for the sake of
simplicity, that the equilibrium
flow velocity and equilibrium plasma current are both zero) to give
Here, the subscript 0 denotes an equilibrium quantity. Perturbed quantities
are written without subscripts. Of course,  ,
, 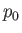 , and
, and 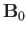 are
constants in a spatially uniform plasma.
are
constants in a spatially uniform plasma.
Let us search for wave-like solutions to Equations (7.26)-(7.29) in which perturbed
quantities vary like
![$ \exp[\,{\rm i}\,({\bf k}\cdot{\bf r}-\omega\,t)]$](img1895.png) .
It follows that
.
It follows that
Assuming that
 , the previous equations yield
, the previous equations yield
Substitution of these expressions into the linearized equation of
motion, Equation (7.31), gives
We can assume, without loss of generality, that the equilibrium magnetic
field, 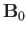 ,
is directed along the
,
is directed along the 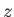 -axis, and that the wavevector,
-axis, and that the wavevector,  , lies
in the
, lies
in the 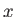 -
-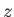 plane. Let
plane. Let 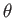 be the angle subtended between
be the angle subtended between 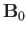 and
and
 . Equation (7.37) reduces to the eigenvalue
equation
. Equation (7.37) reduces to the eigenvalue
equation
![$\displaystyle \left( \begin{array}{ccc} { \omega^2 - k^2\,V_A^{\,2} -k^2\,V_S^{...
...eft(\begin{array}{c}V_x\\ [0.5ex] V_y\\ [0.5ex] V_z\end{array}\right) = {\bf0}.$](img2298.png) |
(7.38) |
Here,
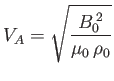 |
(7.39) |
is the Alfvén speed, and
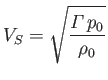 |
(7.40) |
is the sound speed. The solubility condition for Equation (7.38) is that
the determinant of the square matrix is zero. This yields the dispersion
relation
![$\displaystyle (\omega^2 - k^2\,V_A^{\,2}\,\cos^2\theta)\left[ \omega^4 - \omega...
...2\,(V_A^{\,2}+V_S^{\,2}) + k^4\,V_A^{\,2}\,V_S^{\,2}\,\cos^2\theta \right] = 0.$](img2301.png) |
(7.41) |
There are three independent roots of the previous dispersion relation,
corresponding to the three different types of wave that can propagate through an
MHD plasma. The first, and most obvious, root is
 |
(7.42) |
which has the associated eigenvector
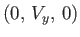 . This
root is characterized by both
. This
root is characterized by both
 and
and
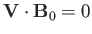 . It immediately follows from Equations (7.34) and (7.35) that there is
zero perturbation of the plasma density or pressure
associated with the root. In fact, this particular root can easily be
identified as the shear-Alfvén wave
introduced in Section 5.8. The properties of the shear-Alfvén wave in a warm (i.e., non-zero
pressure) plasma are unchanged from those found earlier in a cold plasma.
Finally, because the shear-Alfvén wave only involves plasma
motion perpendicular to the magnetic field, we would expect the
dispersion relation (7.42) to hold good in a collisionless, as well as a
collisional, plasma.
. It immediately follows from Equations (7.34) and (7.35) that there is
zero perturbation of the plasma density or pressure
associated with the root. In fact, this particular root can easily be
identified as the shear-Alfvén wave
introduced in Section 5.8. The properties of the shear-Alfvén wave in a warm (i.e., non-zero
pressure) plasma are unchanged from those found earlier in a cold plasma.
Finally, because the shear-Alfvén wave only involves plasma
motion perpendicular to the magnetic field, we would expect the
dispersion relation (7.42) to hold good in a collisionless, as well as a
collisional, plasma.
The remaining two roots of the dispersion relation (7.41) are written
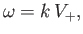 |
(7.43) |
and
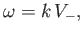 |
(7.44) |
respectively.
Here,
![$\displaystyle V_\pm = \left\{\frac{1}{2}\left[V_A^{\,2} + V_S^{\,2} \pm \sqrt{ ...
...{\,2})^{\,2} - 4\, V_A^{\,2}\,V_S^{\,2}\,\cos^2\theta} \,\right]\right\}^{1/2}.$](img2308.png) |
(7.45) |
Note that
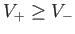 . The first root is generally termed the
fast magnetosonic wave, or fast wave, for short, whereas
the second root is usually called the slow magnetosonic
wave, or slow wave. The eigenvectors for these waves are
. The first root is generally termed the
fast magnetosonic wave, or fast wave, for short, whereas
the second root is usually called the slow magnetosonic
wave, or slow wave. The eigenvectors for these waves are
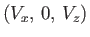 . It follows that
. It follows that
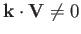 and
and
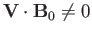 . Hence, these waves are associated with non-zero perturbations
in the plasma density and pressure, and also involve plasma motion parallel, as
well as perpendicular, to the magnetic field. The latter observation suggests
that the dispersion relations
(7.43) and (7.44) are likely to undergo significant modification in
collisionless plasmas.
. Hence, these waves are associated with non-zero perturbations
in the plasma density and pressure, and also involve plasma motion parallel, as
well as perpendicular, to the magnetic field. The latter observation suggests
that the dispersion relations
(7.43) and (7.44) are likely to undergo significant modification in
collisionless plasmas.
In order to better understand the nature of the fast and slow waves, let us
consider the cold plasma limit, which is obtained by letting the sound
speed, 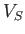 , tend to zero. In this limit, the slow wave ceases to exist (in fact,
its phase-velocity tends to zero), whereas the dispersion relation for
the fast wave reduces to
, tend to zero. In this limit, the slow wave ceases to exist (in fact,
its phase-velocity tends to zero), whereas the dispersion relation for
the fast wave reduces to
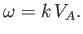 |
(7.46) |
This can be identified as the dispersion relation for the
compressional-Alfvén wave introduced in Section 5.8.
Thus, we can identify the fast wave as the compressional-Alfvén wave
modified by a non-zero plasma pressure.
In the limit
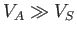 , which is appropriate to low-
, which is appropriate to low- plasmas (see
Section 4.15), the dispersion relation for the slow wave reduces to
plasmas (see
Section 4.15), the dispersion relation for the slow wave reduces to
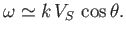 |
(7.47) |
This is actually the dispersion relation of a sound wave propagating
along magnetic field-lines. Thus, in low- plasmas, the slow
wave is a sound wave modified by the presence of the magnetic field.
plasmas, the slow
wave is a sound wave modified by the presence of the magnetic field.
The distinction between the fast and slow waves can be further understood
by comparing the signs of the wave-induced fluctuations in the plasma and magnetic
pressures: 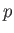 and
and
 , respectively.
It follows from Equation (7.36) that
, respectively.
It follows from Equation (7.36) that
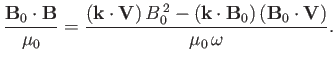 |
(7.48) |
Now, the 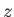 -component of Equation (7.31) yields
-component of Equation (7.31) yields
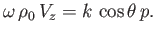 |
(7.49) |
Combining Equations (7.35), (7.39), (7.40), (7.48), and (7.49), we obtain
 |
(7.50) |
Hence, 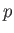 and
and
 have the same sign
if
have the same sign
if
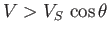 , and the opposite sign if
, and the opposite sign if
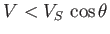 . Here,
. Here,
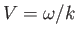 is the phase-velocity. It is
straightforward to show that
is the phase-velocity. It is
straightforward to show that
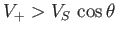 , and
, and
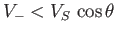 .
Thus, we conclude that the plasma pressure and
magnetic pressure fluctuations reinforce one another in the fast magnetosonic wave, whereas the
fluctuations oppose one another in the slow magnetosonic wave.
.
Thus, we conclude that the plasma pressure and
magnetic pressure fluctuations reinforce one another in the fast magnetosonic wave, whereas the
fluctuations oppose one another in the slow magnetosonic wave.
Figure:
Schematic diagram showing the variation of the phase velocities of the three MHD waves with direction of propagation in the 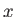 -
-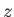 plane.
plane.
 |
Figure 7.1 shows the variation of the phase velocities of the three MHD waves with direction of propagation in the
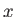 -
-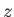 plane for a low-
plane for a low- plasma in which
plasma in which  . It can be
seen that the slow wave always has a smaller phase-velocity than the
shear-Alfvén wave, which, in turn, always has a smaller phase-velocity than the fast wave.
. It can be
seen that the slow wave always has a smaller phase-velocity than the
shear-Alfvén wave, which, in turn, always has a smaller phase-velocity than the fast wave.
The existence of MHD waves was first predicted theoretically by Alfvén (Alfvén 1942). These
waves were subsequently observed in the laboratory--first in magnetized conducting fluids (e.g., mercury) (Lundquist 1949), and
then in magnetized plasmas (Wilcox, Boley, and DeSilva 1960).



Next: Solar Wind
Up: Magnetohydrodynamic Fluids
Previous: Flux Freezing
Richard Fitzpatrick
2016-01-23
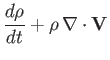
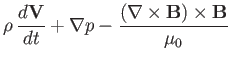
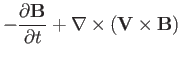
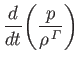
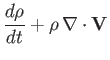
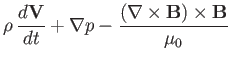
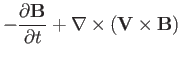
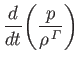
![]() .
It follows that
.
It follows that
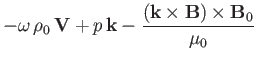

![]() ,
is directed along the
,
is directed along the ![]() -axis, and that the wavevector,
-axis, and that the wavevector, ![]() , lies
in the
, lies
in the ![]() -
-![]() plane. Let
plane. Let ![]() be the angle subtended between
be the angle subtended between ![]() and
and
![]() . Equation (7.37) reduces to the eigenvalue
equation
. Equation (7.37) reduces to the eigenvalue
equation
![]() , tend to zero. In this limit, the slow wave ceases to exist (in fact,
its phase-velocity tends to zero), whereas the dispersion relation for
the fast wave reduces to
, tend to zero. In this limit, the slow wave ceases to exist (in fact,
its phase-velocity tends to zero), whereas the dispersion relation for
the fast wave reduces to
![]() , which is appropriate to low-
, which is appropriate to low-![]() plasmas (see
Section 4.15), the dispersion relation for the slow wave reduces to
plasmas (see
Section 4.15), the dispersion relation for the slow wave reduces to
![]() and
and
![]() , respectively.
It follows from Equation (7.36) that
, respectively.
It follows from Equation (7.36) that


![]() -
-![]() plane for a low-
plane for a low-![]() plasma in which
plasma in which ![]() . It can be
seen that the slow wave always has a smaller phase-velocity than the
shear-Alfvén wave, which, in turn, always has a smaller phase-velocity than the fast wave.
. It can be
seen that the slow wave always has a smaller phase-velocity than the
shear-Alfvén wave, which, in turn, always has a smaller phase-velocity than the fast wave.