


Next: Parker Model of Solar
Up: Magnetohydrodynamic Fluids
Previous: MHD Waves
The solar wind is a high-speed particle stream continuously blown out from
the Sun into interplanetary space (Priest 1984). It extends far beyond the orbit
of the Earth, and terminates in a shock front, called the heliopause,
where it interfaces with the weakly ionized interstellar medium. The heliopause
is predicted to lie between 110 and
160 AU (1 astronomical unit, which is the mean Earth-Sun distance, is
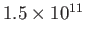 m)
from the center of the Sun (Suess 1990).
The Voyager 1 spacecraft is inferred to have crossed the heliopause in August of 2012 (Webber and McDonald 2013).
m)
from the center of the Sun (Suess 1990).
The Voyager 1 spacecraft is inferred to have crossed the heliopause in August of 2012 (Webber and McDonald 2013).
In the vicinity of the Earth, (i.e., at about 1 AU from the
Sun), the solar wind velocity typically
ranges between 300 and 1400
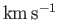 (Priest 1984). The average value
is approximately
(Priest 1984). The average value
is approximately
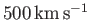 , which corresponds to about a
4 day time-of-flight from the Sun. Note that the solar wind is
both super-sonic and super-Alfvénic, and is predominately composed of protons and electrons.
, which corresponds to about a
4 day time-of-flight from the Sun. Note that the solar wind is
both super-sonic and super-Alfvénic, and is predominately composed of protons and electrons.
The solar wind was predicted
theoretically by Eugine Parker (Parker 1958)
a number of years before its
existence
was confirmed by means of satellite data (Neugebauer and Snyder 1966). Parker's prediction of a super-sonic
outflow of gas from the Sun is a
fascinating application
of plasma physics.
The solar wind originates from the solar corona, which
is a hot, tenuous plasma, surrounding the Sun, with characteristic temperatures and
particle densities of about 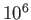 K and
K and
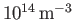 ,
respectively (Priest 1984). The corona is actually far hotter than the solar
atmosphere, or photosphere. In fact, the
temperature of the photosphere is only about
,
respectively (Priest 1984). The corona is actually far hotter than the solar
atmosphere, or photosphere. In fact, the
temperature of the photosphere is only about 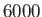 K. It is
thought that the corona is heated by Alfvén waves emanating from the
photosphere (Priest 1984). The solar corona is most easily observed during a total
solar eclipse, when it is visible as a white filamentary region
immediately surrounding the Sun.
K. It is
thought that the corona is heated by Alfvén waves emanating from the
photosphere (Priest 1984). The solar corona is most easily observed during a total
solar eclipse, when it is visible as a white filamentary region
immediately surrounding the Sun.
Let us start, following Chapman (Chapman 1957), by attempting
to construct a model for a static solar corona. The equation
of hydrostatic equilibrium for the corona takes the form
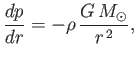 |
(7.51) |
where
 is the gravitational constant,
is the gravitational constant,
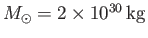 the solar mass (Yoder 1995), and
the solar mass (Yoder 1995), and  the radial distance from the center of the Sun.
The plasma density is written
the radial distance from the center of the Sun.
The plasma density is written
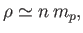 |
(7.52) |
where 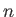 is the number
density of protons. If both protons and electrons are assumed
to possess a common temperature,
is the number
density of protons. If both protons and electrons are assumed
to possess a common temperature, 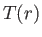 , then the coronal pressure is
given by
, then the coronal pressure is
given by
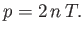 |
(7.53) |
The thermal conductivity of the corona is dominated by the electron thermal
conductivity, and takes the form [see Equations (4.89) and (4.108)]
 |
(7.54) |
where 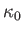 is a relatively weak function of density and
temperature. For typical coronal conditions, this conductivity is
extremely high. In fact, it is about twenty times the thermal
conductivity of copper at room temperature. The coronal heat flux density
is written
is a relatively weak function of density and
temperature. For typical coronal conditions, this conductivity is
extremely high. In fact, it is about twenty times the thermal
conductivity of copper at room temperature. The coronal heat flux density
is written
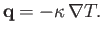 |
(7.55) |
For a static corona, in the absence of energy sources or sinks, we require
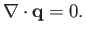 |
(7.56) |
Assuming spherical symmetry, this expression reduces to (Huba 2000b)
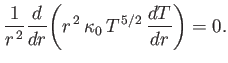 |
(7.57) |
Adopting the sensible boundary condition that the coronal temperature must
tend to zero at large distances from the Sun, we obtain
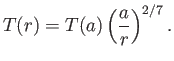 |
(7.58) |
The reference level  is conveniently taken to be the
base of the corona, where
is conveniently taken to be the
base of the corona, where
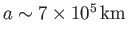 ,
,
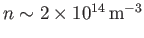 , and
, and
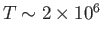 K (Priest 1984).
K (Priest 1984).
Equations (7.51), (7.52), (7.53), and (7.58) can be combined and
integrated to give
![$\displaystyle p(r) = p(a) \exp\left\{\frac{7}{5}\,\frac{G\,M_\odot\,m_p}{2\,T(a)\,a} \left[\left(\frac{a}{r}\right)^{5/7}-1\right]\right\}.$](img2347.png) |
(7.59) |
Observe that, as
 , the coronal pressure tends towards a finite
constant value:
, the coronal pressure tends towards a finite
constant value:
![$\displaystyle p(\infty) = p(a)\,\exp\left[-\frac{7}{5}\,\frac{G\,M_\odot\,m_p}{2\,T(a)\,a} \right] = p(a)\,\exp\left[-\frac{14}{5}\,\frac{T_0}{T(a)}\right],$](img2349.png) |
(7.60) |
where 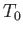 is defined in Equation (7.66).
There is, of course, nothing at large distances from the Sun that could
contain such a pressure (the pressure of the interstellar medium is
negligibly small). Thus, we conclude, following Parker, that the
static coronal model is unphysical.
is defined in Equation (7.66).
There is, of course, nothing at large distances from the Sun that could
contain such a pressure (the pressure of the interstellar medium is
negligibly small). Thus, we conclude, following Parker, that the
static coronal model is unphysical.
We have just demonstrated that a static model of the solar corona is
unsatisfactory. Let us, instead, attempt to construct a dynamic model
in which material flows outward from the Sun.



Next: Parker Model of Solar
Up: Magnetohydrodynamic Fluids
Previous: MHD Waves
Richard Fitzpatrick
2016-01-23
![]() (Priest 1984). The average value
is approximately
(Priest 1984). The average value
is approximately
![]() , which corresponds to about a
4 day time-of-flight from the Sun. Note that the solar wind is
both super-sonic and super-Alfvénic, and is predominately composed of protons and electrons.
, which corresponds to about a
4 day time-of-flight from the Sun. Note that the solar wind is
both super-sonic and super-Alfvénic, and is predominately composed of protons and electrons.
![]() K and
K and
![]() ,
respectively (Priest 1984). The corona is actually far hotter than the solar
atmosphere, or photosphere. In fact, the
temperature of the photosphere is only about
,
respectively (Priest 1984). The corona is actually far hotter than the solar
atmosphere, or photosphere. In fact, the
temperature of the photosphere is only about ![]() K. It is
thought that the corona is heated by Alfvén waves emanating from the
photosphere (Priest 1984). The solar corona is most easily observed during a total
solar eclipse, when it is visible as a white filamentary region
immediately surrounding the Sun.
K. It is
thought that the corona is heated by Alfvén waves emanating from the
photosphere (Priest 1984). The solar corona is most easily observed during a total
solar eclipse, when it is visible as a white filamentary region
immediately surrounding the Sun.
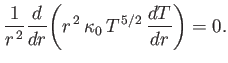
![$\displaystyle p(r) = p(a) \exp\left\{\frac{7}{5}\,\frac{G\,M_\odot\,m_p}{2\,T(a)\,a} \left[\left(\frac{a}{r}\right)^{5/7}-1\right]\right\}.$](img2347.png)
![$\displaystyle p(\infty) = p(a)\,\exp\left[-\frac{7}{5}\,\frac{G\,M_\odot\,m_p}{2\,T(a)\,a} \right] = p(a)\,\exp\left[-\frac{14}{5}\,\frac{T_0}{T(a)}\right],$](img2349.png)