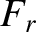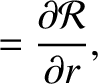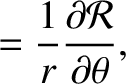Let
 be the angular velocity of precession of Mercury's eccentricity vector,
be the angular velocity of precession of Mercury's eccentricity vector, 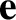 . It follows that [see Equation (A.96)]
which can be inverted to give
. It follows that [see Equation (A.96)]
which can be inverted to give
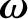 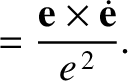 |
(B.7) |
Here, we have assumed, without loss of generality, that
 is normal to
is normal to 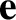 (because any parallel component of
(because any parallel component of
 would
have no effect on the time evolution of
would
have no effect on the time evolution of 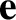 ).
).
Consider a Cartesian coordinate system  ,
,  ,
,  that is instantaneously aligned with the orbit of Mercury, in such a manner
that
that is instantaneously aligned with the orbit of Mercury, in such a manner
that
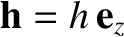 and
and
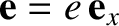 . Thus, the orbital plane coincides with the
. Thus, the orbital plane coincides with the  -
- plane, and
the perihelion lies (instantaneously) on the
plane, and
the perihelion lies (instantaneously) on the  -axis.
Because the eccentricity vector is always directed toward Mercury's perihelion, the rate of perihelion precession is equivalent
to the component of
-axis.
Because the eccentricity vector is always directed toward Mercury's perihelion, the rate of perihelion precession is equivalent
to the component of
 that is normal to the orbital plane. In other words,
that is normal to the orbital plane. In other words,
Note that any component of
 that lies in the orbital plane would cause the orientation of this plane to evolve in time.
In the following, we shall neglect this effect because it has a negligible influence on Mercury's perihelion precession rate
(given Mercury's small orbital eccentricity, as well as its small orbital inclination with respect to the orbits of the other planets
in the solar system.)
that lies in the orbital plane would cause the orientation of this plane to evolve in time.
In the following, we shall neglect this effect because it has a negligible influence on Mercury's perihelion precession rate
(given Mercury's small orbital eccentricity, as well as its small orbital inclination with respect to the orbits of the other planets
in the solar system.)
Let  ,
,  ,
,  be a cylindrical coordinate system in the (
be a cylindrical coordinate system in the ( ,
,  ,
,  ) frame. Mercury's orbital
plane thus corresponds to
) frame. Mercury's orbital
plane thus corresponds to  . Moreover, we can
write (see Section 4.4)
. Moreover, we can
write (see Section 4.4)
as well as
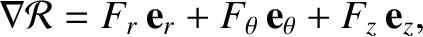 |
(B.11) |
where the Cartesian components of the unit vectors 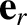 ,
,
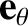 , and
, and 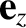 are
Furthermore,
are
Furthermore,
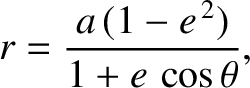 |
(B.15) |
where  is Mercury's orbital major radius. (See Section 4.8.)
Incidentally, the angle
is Mercury's orbital major radius. (See Section 4.8.)
Incidentally, the angle  is
Mercury's true anomaly. (See Section 4.11.).
It follows from Equations (B.5) and (B.9)–(B.11) that
is
Mercury's true anomaly. (See Section 4.11.).
It follows from Equations (B.5) and (B.9)–(B.11) that
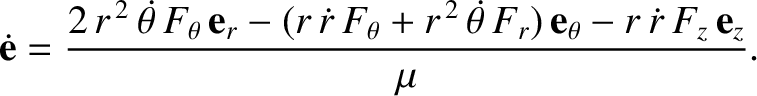 |
(B.16) |
Moreover, Equations (B.8) and (B.12)–(B.13) yield
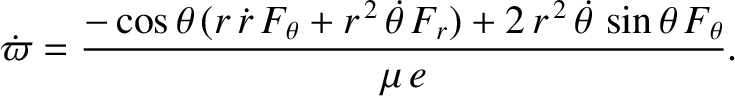 |
(B.17) |
However, differentiation of Equation (B.16) with respect to time gives
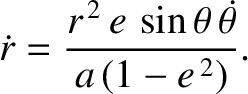 |
(B.18) |
Thus, we obtain
![$\displaystyle \dot{\varpi} =- \frac{r^{\,2}\,\skew{5}\dot{\theta}}{\mu\,e}\left...
...\sin\theta\left(\frac{2+e\,\cos\theta}{1+e\,\cos\theta}\right)F_\theta
\right].$](img4161.png) |
(B.19) |
Finally, from Equation (B.11),
which yields
![$\displaystyle \dot{\varpi} = -\frac{r^{\,2}\,\skew{5}\dot{\theta}}{\mu\,e}\left...
...e\,\cos\theta}\right)\frac{1}{r}\frac{\partial{\cal R}}{\partial\theta}\right].$](img4164.png) |
(B.22) |
 be the angular velocity of precession of Mercury's eccentricity vector,
be the angular velocity of precession of Mercury's eccentricity vector,  . It follows that [see Equation (A.96)]
. It follows that [see Equation (A.96)]
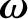
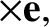
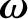
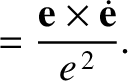
 is normal to
is normal to 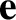 (because any parallel component of
(because any parallel component of
 would
have no effect on the time evolution of
would
have no effect on the time evolution of 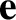 ).
).
 ,
,  ,
,  that is instantaneously aligned with the orbit of Mercury, in such a manner
that
that is instantaneously aligned with the orbit of Mercury, in such a manner
that
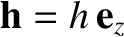 and
and
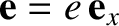 . Thus, the orbital plane coincides with the
. Thus, the orbital plane coincides with the  -
- plane, and
the perihelion lies (instantaneously) on the
plane, and
the perihelion lies (instantaneously) on the  -axis.
Because the eccentricity vector is always directed toward Mercury's perihelion, the rate of perihelion precession is equivalent
to the component of
-axis.
Because the eccentricity vector is always directed toward Mercury's perihelion, the rate of perihelion precession is equivalent
to the component of
 that is normal to the orbital plane. In other words,
that is normal to the orbital plane. In other words,
 that lies in the orbital plane would cause the orientation of this plane to evolve in time.
In the following, we shall neglect this effect because it has a negligible influence on Mercury's perihelion precession rate
(given Mercury's small orbital eccentricity, as well as its small orbital inclination with respect to the orbits of the other planets
in the solar system.)
that lies in the orbital plane would cause the orientation of this plane to evolve in time.
In the following, we shall neglect this effect because it has a negligible influence on Mercury's perihelion precession rate
(given Mercury's small orbital eccentricity, as well as its small orbital inclination with respect to the orbits of the other planets
in the solar system.)
 ,
,  ,
,  be a cylindrical coordinate system in the (
be a cylindrical coordinate system in the ( ,
,  ,
,  ) frame. Mercury's orbital
plane thus corresponds to
) frame. Mercury's orbital
plane thus corresponds to  . Moreover, we can
write (see Section 4.4)
. Moreover, we can
write (see Section 4.4)
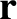
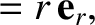
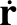
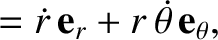
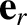 ,
,
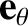 , and
, and 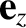 are
Furthermore,
where
are
Furthermore,
where  is Mercury's orbital major radius. (See Section 4.8.)
Incidentally, the angle
is Mercury's orbital major radius. (See Section 4.8.)
Incidentally, the angle  is
Mercury's true anomaly. (See Section 4.11.).
It follows from Equations (B.5) and (B.9)–(B.11) that
is
Mercury's true anomaly. (See Section 4.11.).
It follows from Equations (B.5) and (B.9)–(B.11) that
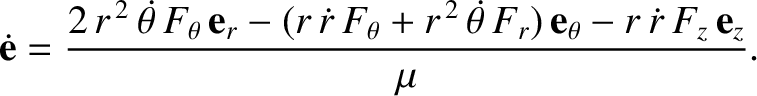
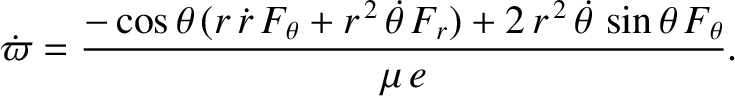
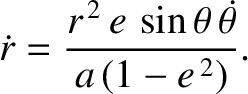
![$\displaystyle \dot{\varpi} =- \frac{r^{\,2}\,\skew{5}\dot{\theta}}{\mu\,e}\left...
...\sin\theta\left(\frac{2+e\,\cos\theta}{1+e\,\cos\theta}\right)F_\theta
\right].$](img4161.png)