Next: Perihelion precession rate Up: Perihelion precession of Mercury Previous: Introduction
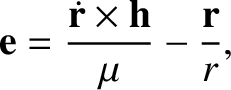 |
(B.3) |
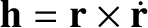 is its orbital angular momentum per unit mass, is of magnitude
is its orbital angular momentum per unit mass, is of magnitude  , and is always directed from the Sun
to Mercury's perihelion. Here,
, and is always directed from the Sun
to Mercury's perihelion. Here,  is the Mercury's orbital eccentricity.
It follows that
is the Mercury's orbital eccentricity.
It follows that
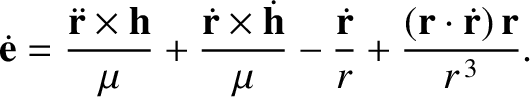 |
(B.4) |
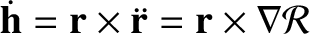 , where use has been made of Equation (B.1).
Hence, making further use of Equation (B.1), the previous expression reduces to
We conclude that the disturbing function causes Mercury's eccentricity vector,
, where use has been made of Equation (B.1).
Hence, making further use of Equation (B.1), the previous expression reduces to
We conclude that the disturbing function causes Mercury's eccentricity vector,  , to evolve in time. Any change in length of
this vector gives rise to a change in Mercury's orbital eccentricity, whereas any change in direction produces a rotation
of Mercury's perihelion. In the following, because we are only interested in the motion of Mercury's perihelion, we shall focus solely on the change in direction (i.e., the precession) of the
, to evolve in time. Any change in length of
this vector gives rise to a change in Mercury's orbital eccentricity, whereas any change in direction produces a rotation
of Mercury's perihelion. In the following, because we are only interested in the motion of Mercury's perihelion, we shall focus solely on the change in direction (i.e., the precession) of the  vector.
vector.