Precession
Suppose that some position vector  precesses (i.e., rotates) about the
precesses (i.e., rotates) about the  -axis at the
angular velocity
-axis at the
angular velocity
 . If
. If 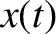 ,
, 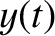 ,
, 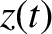 are the Cartesian components of
are the Cartesian components of  at time
at time 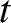 then it follows from the analysis in the previous section that
then it follows from the analysis in the previous section that
![$\displaystyle \left(\begin{array}{c}x(t)\\ [0.5ex]y(t)\\ [0.5ex]z(t)\end{array}...
...right)\left(\begin{array}{c}x(0)\\ [0.5ex]y(0)\\ [0.5ex]z(0)\end{array}\right).$](img3964.png) |
(A.93) |
Hence, making use of the small angle approximations to the sine and cosine functions, we obtain
![$\displaystyle \left(\begin{array}{c}x(\delta t)\\ [0.5ex]y(\delta t)\\ [0.5ex]z...
...right)\left(\begin{array}{c}x(0)\\ [0.5ex]y(0)\\ [0.5ex]z(0)\end{array}\right),$](img3965.png) |
(A.94) |
which immediately implies that
![$\displaystyle \left(\begin{array}{c}\dot{x}\\ [0.5ex]\dot{y}\\ [0.5ex]\dot{z}\e...
...d{array}\right)\left(\begin{array}{c}x\\ [0.5ex]y\\ [0.5ex]z\end{array}\right),$](img3966.png) |
(A.95) |
or
where

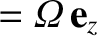 is the angular velocity of precession. Because vector
equations are coordinate independent, we deduce that the preceding expression is the general equation for the time evolution of
a position vector
is the angular velocity of precession. Because vector
equations are coordinate independent, we deduce that the preceding expression is the general equation for the time evolution of
a position vector  that precesses at the angular velocity
that precesses at the angular velocity
 .
.
 precesses (i.e., rotates) about the
precesses (i.e., rotates) about the  -axis at the
angular velocity
-axis at the
angular velocity
 . If
. If 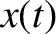 ,
, 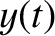 ,
, 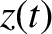 are the Cartesian components of
are the Cartesian components of  at time
at time  then it follows from the analysis in the previous section that
then it follows from the analysis in the previous section that
![$\displaystyle \left(\begin{array}{c}x(t)\\ [0.5ex]y(t)\\ [0.5ex]z(t)\end{array}...
...right)\left(\begin{array}{c}x(0)\\ [0.5ex]y(0)\\ [0.5ex]z(0)\end{array}\right).$](img3964.png)
![$\displaystyle \left(\begin{array}{c}x(\delta t)\\ [0.5ex]y(\delta t)\\ [0.5ex]z...
...right)\left(\begin{array}{c}x(0)\\ [0.5ex]y(0)\\ [0.5ex]z(0)\end{array}\right),$](img3965.png)
![$\displaystyle \left(\begin{array}{c}\dot{x}\\ [0.5ex]\dot{y}\\ [0.5ex]\dot{z}\e...
...d{array}\right)\left(\begin{array}{c}x\\ [0.5ex]y\\ [0.5ex]z\end{array}\right),$](img3966.png)

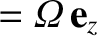 is the angular velocity of precession. Because vector
equations are coordinate independent, we deduce that the preceding expression is the general equation for the time evolution of
a position vector
is the angular velocity of precession. Because vector
equations are coordinate independent, we deduce that the preceding expression is the general equation for the time evolution of
a position vector  that precesses at the angular velocity
that precesses at the angular velocity
 .
.