Next, let us consider terms in the solution of the lunar equations of motions that depend linearly on the lunar inclination,  .
.
According to Equation (11.155),
 |
(11.305) |
It follows from Equations (11.209), (11.213), and (11.217) that
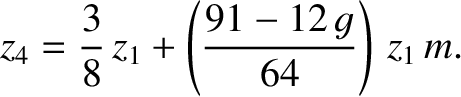 |
(11.306) |
According to Equation (11.156),
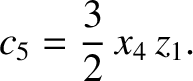 |
(11.307) |
It follows from Equations (11.209), (11.214), and (11.217) that
 |
(11.308) |
According to Equation (11.152),
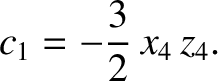 |
(11.309) |
It follows from Equation (11.217), as well as the previous expression for 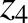 , that
, that
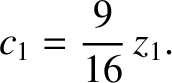 |
(11.310) |
The preceding expression can be combined with Equation (11.208) to give
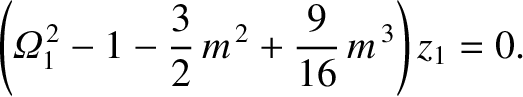 |
(11.311) |
The non-trivial solution of this equation is such that
 |
(11.312) |
It follows from Equation (11.210) that
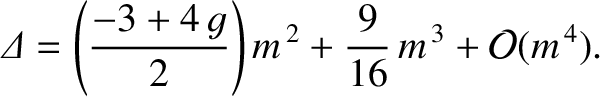 |
(11.313) |
Thus, setting
 , we get
, we get
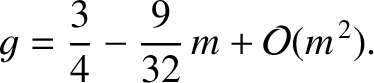 |
(11.314) |
The arbitrary parameter 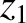 is chosen such that the parameter
is chosen such that the parameter 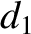 , appearing in
Equation (11.124), is the same as in the undisturbed motion. Thus, making use of Equation (11.184),
, appearing in
Equation (11.124), is the same as in the undisturbed motion. Thus, making use of Equation (11.184),
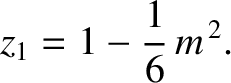 |
(11.315) |
Hence, Equations (11.306) and (11.308) reduce to
It follows from Equations (11.122)–(11.124), (11.184), (11.187), and (11.188), as well as the previous expressions for 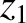 ,
, 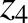 ,
and
,
and 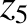 , that the net perturbation to the lunar orbit
due to terms in the solution of the lunar equations of motion that depend linearly on
, that the net perturbation to the lunar orbit
due to terms in the solution of the lunar equations of motion that depend linearly on  is
is
The previous expressions are accurate to
 .
.
The first term on the right-hand side of expression (11.320) is Keplerian in origin (i.e., it is independent of the perturbing
influence of the Sun).
The second term, which is known as evection in latitude, is due to the
combined action of the Sun and the inclination of the lunar orbit to the ecliptic. Evection in latitude can be thought of as causing a slight increase in the inclination of the lunar orbit
at the times of the first and last quarter moons (i.e., when
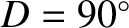 and
and
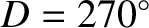 ), and a slight decrease at the times of the new moon and
the full moon (i.e., when
), and a slight decrease at the times of the new moon and
the full moon (i.e., when 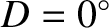 and
and
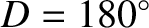 ). (See Section 11.18, Exercise 4.) Evection in latitude generates a perturbation in the lunar ecliptic latitude that oscillates sinusoidally with a period of 32.3 days, and has
an amplitude (calculated with
). (See Section 11.18, Exercise 4.) Evection in latitude generates a perturbation in the lunar ecliptic latitude that oscillates sinusoidally with a period of 32.3 days, and has
an amplitude (calculated with 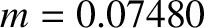 and
and
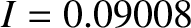 ) of 602 arc seconds. As before, the oscillation period is in good agreement with observations, but the
amplitude is somewhat inaccurate [it should be 624 arc seconds (Chapront-Touzé and Chapront 1988)] due to the omission of higher order (in
) of 602 arc seconds. As before, the oscillation period is in good agreement with observations, but the
amplitude is somewhat inaccurate [it should be 624 arc seconds (Chapront-Touzé and Chapront 1988)] due to the omission of higher order (in  and
and  ) contributions.
) contributions.
 .
.

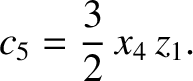
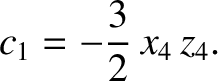
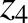 , that
, that
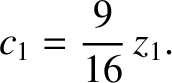
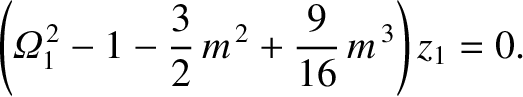

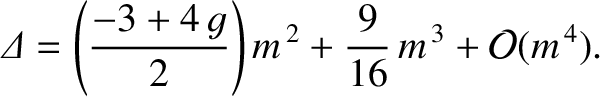
 , we get
The arbitrary parameter
, we get
The arbitrary parameter 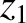 is chosen such that the parameter
is chosen such that the parameter 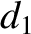 , appearing in
Equation (11.124), is the same as in the undisturbed motion. Thus, making use of Equation (11.184),
Hence, Equations (11.306) and (11.308) reduce to
, appearing in
Equation (11.124), is the same as in the undisturbed motion. Thus, making use of Equation (11.184),
Hence, Equations (11.306) and (11.308) reduce to
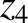
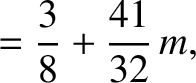
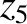
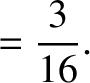
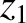 ,
, 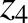 ,
and
,
and 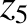 , that the net perturbation to the lunar orbit
due to terms in the solution of the lunar equations of motion that depend linearly on
, that the net perturbation to the lunar orbit
due to terms in the solution of the lunar equations of motion that depend linearly on  is
is
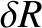
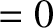

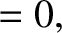
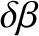

 .
.
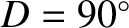 and
and
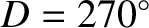 ), and a slight decrease at the times of the new moon and
the full moon (i.e., when
), and a slight decrease at the times of the new moon and
the full moon (i.e., when 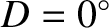 and
and
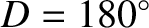 ). (See Section 11.18, Exercise 4.) Evection in latitude generates a perturbation in the lunar ecliptic latitude that oscillates sinusoidally with a period of 32.3 days, and has
an amplitude (calculated with
). (See Section 11.18, Exercise 4.) Evection in latitude generates a perturbation in the lunar ecliptic latitude that oscillates sinusoidally with a period of 32.3 days, and has
an amplitude (calculated with 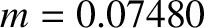 and
and
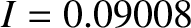 ) of 602 arc seconds. As before, the oscillation period is in good agreement with observations, but the
amplitude is somewhat inaccurate [it should be 624 arc seconds (Chapront-Touzé and Chapront 1988)] due to the omission of higher order (in
) of 602 arc seconds. As before, the oscillation period is in good agreement with observations, but the
amplitude is somewhat inaccurate [it should be 624 arc seconds (Chapront-Touzé and Chapront 1988)] due to the omission of higher order (in  and
and  ) contributions.
) contributions.