Next: Derivation of lunar equations Up: Lunar motion Previous: Earth–Moon–Sun system
 -
- plane. This implies that the
plane. This implies that the
 -
- plane corresponds to the so-called ecliptic plane. Approximating the solar orbit as a low-eccentricity Keplerian orbit,
we can write
where
plane corresponds to the so-called ecliptic plane. Approximating the solar orbit as a low-eccentricity Keplerian orbit,
we can write
where
 , and
, and
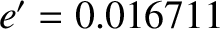 is the orbital eccentricity (Yoder 1995). (See Section 4.13.) Here, we have
neglected terms that are
is the orbital eccentricity (Yoder 1995). (See Section 4.13.) Here, we have
neglected terms that are
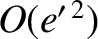 , and smaller.
, and smaller.