Next: Electrostatic Energy Up: Electrostatic Fields Previous: Gauss's Law
 th particle in the
electric field,
th particle in the
electric field,
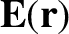 , generated by all of the other static particles.
The equilibrium position of the
, generated by all of the other static particles.
The equilibrium position of the  th particle corresponds to some
point of displacement
th particle corresponds to some
point of displacement  at which
at which
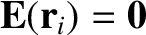 , because this implies that the particle is not
subject to an electrical force. By implication,
, because this implies that the particle is not
subject to an electrical force. By implication,
 does not correspond to the equilibrium displacement of
any other particle in the system.
However, in order
for
does not correspond to the equilibrium displacement of
any other particle in the system.
However, in order
for  to be the displacement of a stable equilibrium point, the
to be the displacement of a stable equilibrium point, the  th particle
must experience a restoring force when its displacement deviates slightly from
th particle
must experience a restoring force when its displacement deviates slightly from  in any direction. Assuming that the
in any direction. Assuming that the
 th particle is (say) positively charged, this implies that the electric
field must be directed radially toward the point whose displacement is
th particle is (say) positively charged, this implies that the electric
field must be directed radially toward the point whose displacement is
 at all neighboring points. Hence,
if we consider a small sphere centered on displacement
at all neighboring points. Hence,
if we consider a small sphere centered on displacement  then there must be a negative flux of
then there must be a negative flux of
 through the surface of this sphere. According to Gauss's law, this necessitates the presence of a negative
charge at displacement
through the surface of this sphere. According to Gauss's law, this necessitates the presence of a negative
charge at displacement  . However, there is no such charge at displacement
. However, there is no such charge at displacement  .
Hence, we conclude that
.
Hence, we conclude that  cannot be directed radially toward the point whose displacement is
cannot be directed radially toward the point whose displacement is  at all neighboring points. In other
words, there must be some neighboring points at which
at all neighboring points. In other
words, there must be some neighboring points at which  is directed away
from the point whose displacement is
is directed away
from the point whose displacement is  . Hence, a positively charged particle
placed at displacement
. Hence, a positively charged particle
placed at displacement  can always escape by moving to such neighboring points.
One corollary of Earnshaw's theorem is that classical electrostatics cannot
account for the stability of atoms and molecules.
can always escape by moving to such neighboring points.
One corollary of Earnshaw's theorem is that classical electrostatics cannot
account for the stability of atoms and molecules.
As an example of the use of Gauss's law, let us calculate the electric field
generated by a spherically symmetric charge annulus of inner radius 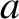 ,
and outer radius
,
and outer radius 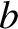 , centered on the origin, and carrying a uniformly
distributed electric charge
, centered on the origin, and carrying a uniformly
distributed electric charge 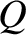 . Now, by symmetry, we expect a spherically
symmetric charge distribution to generate a spherically symmetric
potential,
. Now, by symmetry, we expect a spherically
symmetric charge distribution to generate a spherically symmetric
potential, 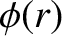 , where
, where  is a spherical polar coordinate. (See Section A.23.) It therefore follows from Equation (2.17) that the electric field is both
spherically symmetric and radial; that is,
is a spherical polar coordinate. (See Section A.23.) It therefore follows from Equation (2.17) that the electric field is both
spherically symmetric and radial; that is,
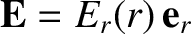 .
Let us apply Gauss's law to an imaginary spherical surface, of radius
.
Let us apply Gauss's law to an imaginary spherical surface, of radius
 , centered on the origin. See Figure 2.4. Such a surface is generally known as a Gaussian surface. According to
Gauss's law, (2.58), the flux of the electric field out of the surface is equal to
the enclosed charge, divided by
, centered on the origin. See Figure 2.4. Such a surface is generally known as a Gaussian surface. According to
Gauss's law, (2.58), the flux of the electric field out of the surface is equal to
the enclosed charge, divided by
 . The flux is easy to calculate because the electric field is everywhere perpendicular to the
surface. We obtain
. The flux is easy to calculate because the electric field is everywhere perpendicular to the
surface. We obtain
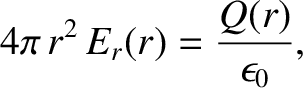 |
(2.59) |
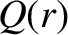 is the charge enclosed by a Gaussian surface of radius
is the charge enclosed by a Gaussian surface of radius  .
However, simple arguments involving proportion reveal that
.
However, simple arguments involving proportion reveal that
![\begin{displaymath}Q(r) = \left\{
\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&r<a\\...
...3)\right] Q&&a\leq r\leq b\\ [0.5ex]
Q&&b<r
\end{array}\right..\end{displaymath}](img1229.png) |
(2.60) |
We can easily determine the electric potential associated with the electric field (2.61) using
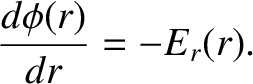 |
(2.62) |
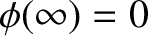 , and that
, and that 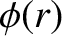 is
continuous at
is
continuous at 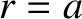 and
and 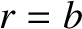 . (Of course, a discontinuous potential would lead to
an infinite electric field, which is unphysical.) It follows that
. (Of course, a discontinuous potential would lead to
an infinite electric field, which is unphysical.) It follows that
![\begin{displaymath}\phi(r) = \left\{
\begin{array}{lcl}
\left[Q/(4\pi\,\epsilon_...
...eq b\\ [0.5ex]
Q/(4\pi\,\epsilon_0\,r)&&b<r
\end{array}\right..\end{displaymath}](img1236.png) |
(2.63) |
![$\displaystyle W = q\left[\phi(0)-\phi(\infty)\right] = \frac{q\,Q}{4\pi\,\epsilon_0}\,\frac{3}{2}\left(\frac{b^2-a^2}{b^3-a^3}\right).$](img1237.png) |
(2.64) |