The interaction of electrically neutral atoms can be modeled using the Lennard-Jones
potential,
![$\displaystyle u(x) = u_0\left[\left(\frac{x_0}{x}\right)^{12}-2\,\left(\frac{x_0}{x}\right)^6\right],$](img4086.png) |
(5.352) |
where 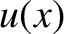 is the potential energy of a pair of atoms when they are a distance
is the potential energy of a pair of atoms when they are a distance  apart, and
apart, and
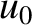 and
and 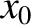 are positive constants. See Figure 5.3. We can think of a given atom in a solid made up of neutral atoms as
a microscopic system interacting with a heat reservoir that consists of all of the other atoms.
Let
are positive constants. See Figure 5.3. We can think of a given atom in a solid made up of neutral atoms as
a microscopic system interacting with a heat reservoir that consists of all of the other atoms.
Let  be the temperature of the reservoir. Let us treat the problem classically, which is equivalent to
assuming that the temperature is sufficiently high that an atom moving in the previous potential is distributed
over a large number of different quantum states. According to a straightforward generalization of the
Boltzmann distribution, (5.329), the mean value of
be the temperature of the reservoir. Let us treat the problem classically, which is equivalent to
assuming that the temperature is sufficiently high that an atom moving in the previous potential is distributed
over a large number of different quantum states. According to a straightforward generalization of the
Boltzmann distribution, (5.329), the mean value of  is
is
![$\displaystyle \langle x\rangle = \frac{\int_0^\infty \exp[-u(x)/(k_B\,T)]\,x\,dx}{\int_0^\infty \exp[-u(x)/(k_B\,T)]\,dx}.$](img4089.png) |
(5.353) |
Figure 5.3:
The Lennard-Jones potential.
|
|
Let us assume that the temperature is sufficiently low that an atom is only likely to be found relatively close to the bottom of the potential well, 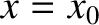 .
We can Taylor expand the potential about
.
We can Taylor expand the potential about 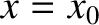 to give
to give
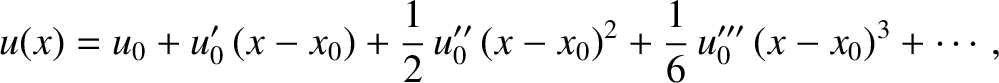 |
(5.354) |
where
Thus, Equation (5.353) gives
![$\displaystyle \langle x\rangle = \frac{\int_{-\infty}^\infty \exp[-u_0''\,y^2/(...
...fty}^\infty \exp[-u_0''\,y^2/(2\,k_B\,T)]\,\exp[-u_0'''\,y^3/(6\,k_B\,T)]\,dy},$](img4100.png) |
(5.359) |
where 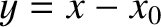 , and we can safely replace the lower limits of integration by
, and we can safely replace the lower limits of integration by  , in the integrals on the right-hand
side of the previous expression, because we are assuming that
the atom is very unlikely to be found a large distance from the bottom of the potential.
Let us further assume that
, in the integrals on the right-hand
side of the previous expression, because we are assuming that
the atom is very unlikely to be found a large distance from the bottom of the potential.
Let us further assume that
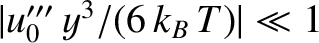 . In this case, we can write
. In this case, we can write
![$\displaystyle \langle x\rangle \simeq x_0+\frac{\int_{-\infty}^\infty \exp[-u_0...
...\infty}^\infty \exp[-u_0''\,y^2/(2\,k_B\,T)]\,[1-u_0'''\,y^3/(6\,k_B\,T)]\,dy}.$](img4104.png) |
(5.360) |
Now,
![$\exp[-u_0''\,y^2/(2\,k_B\,T)]$](img4105.png) and
and 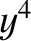 are even functions of
are even functions of  , whereas
, whereas  and
and 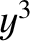 are odd functions.
In general, an integral over all
are odd functions.
In general, an integral over all  of the product of an even and an odd function averages to zero, whereas
an integral of the product of two even functions does not. Hence, the previous equation simplifies to
give
However,
of the product of an even and an odd function averages to zero, whereas
an integral of the product of two even functions does not. Hence, the previous equation simplifies to
give
However,
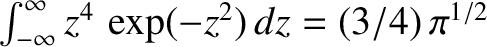 , and
, and
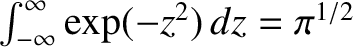 ,
so we get
,
so we get
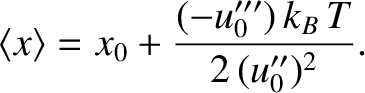 |
(5.362) |
Note that
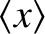 increases linearly with increasing temperature.
increases linearly with increasing temperature.
The coefficient of linear thermal expansion of a solid is defined
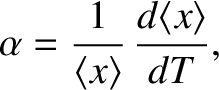 |
(5.363) |
where
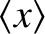 is the mean distance between nearest neighbor atoms.
The previous two equations yield
is the mean distance between nearest neighbor atoms.
The previous two equations yield
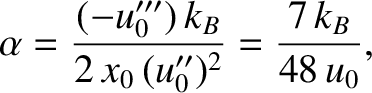 |
(5.364) |
where use has been made of Equations (5.357) and (5.358).
For solid argon at 80 K,
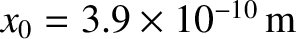 , and
, and
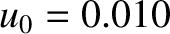 eV. Hence, we deduce
that
eV. Hence, we deduce
that
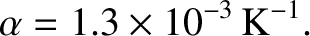 |
(5.365) |
The measured value of  is about
is about
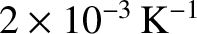 .
.
![$\displaystyle u(x) = u_0\left[\left(\frac{x_0}{x}\right)^{12}-2\,\left(\frac{x_0}{x}\right)^6\right],$](img4086.png)
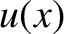 is the potential energy of a pair of atoms when they are a distance
is the potential energy of a pair of atoms when they are a distance  apart, and
apart, and
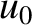 and
and 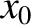 are positive constants. See Figure 5.3. We can think of a given atom in a solid made up of neutral atoms as
a microscopic system interacting with a heat reservoir that consists of all of the other atoms.
Let
are positive constants. See Figure 5.3. We can think of a given atom in a solid made up of neutral atoms as
a microscopic system interacting with a heat reservoir that consists of all of the other atoms.
Let  be the temperature of the reservoir. Let us treat the problem classically, which is equivalent to
assuming that the temperature is sufficiently high that an atom moving in the previous potential is distributed
over a large number of different quantum states. According to a straightforward generalization of the
Boltzmann distribution, (5.329), the mean value of
be the temperature of the reservoir. Let us treat the problem classically, which is equivalent to
assuming that the temperature is sufficiently high that an atom moving in the previous potential is distributed
over a large number of different quantum states. According to a straightforward generalization of the
Boltzmann distribution, (5.329), the mean value of  is
is
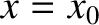 .
We can Taylor expand the potential about
.
We can Taylor expand the potential about 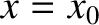 to give
to give
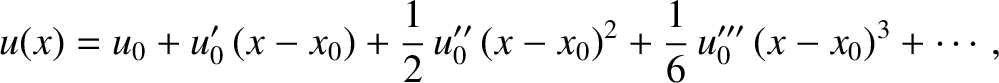
![$\displaystyle \langle x\rangle = \frac{\int_{-\infty}^\infty \exp[-u_0''\,y^2/(...
...fty}^\infty \exp[-u_0''\,y^2/(2\,k_B\,T)]\,\exp[-u_0'''\,y^3/(6\,k_B\,T)]\,dy},$](img4100.png)
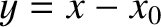 , and we can safely replace the lower limits of integration by
, and we can safely replace the lower limits of integration by  , in the integrals on the right-hand
side of the previous expression, because we are assuming that
the atom is very unlikely to be found a large distance from the bottom of the potential.
Let us further assume that
, in the integrals on the right-hand
side of the previous expression, because we are assuming that
the atom is very unlikely to be found a large distance from the bottom of the potential.
Let us further assume that
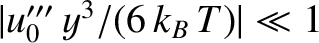 . In this case, we can write
. In this case, we can write
![$\displaystyle \langle x\rangle \simeq x_0+\frac{\int_{-\infty}^\infty \exp[-u_0...
...\infty}^\infty \exp[-u_0''\,y^2/(2\,k_B\,T)]\,[1-u_0'''\,y^3/(6\,k_B\,T)]\,dy}.$](img4104.png)
![$\exp[-u_0''\,y^2/(2\,k_B\,T)]$](img4105.png) and
and 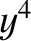 are even functions of
are even functions of  , whereas
, whereas  and
and 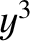 are odd functions.
In general, an integral over all
are odd functions.
In general, an integral over all  of the product of an even and an odd function averages to zero, whereas
an integral of the product of two even functions does not. Hence, the previous equation simplifies to
give
of the product of an even and an odd function averages to zero, whereas
an integral of the product of two even functions does not. Hence, the previous equation simplifies to
give
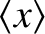
![$\displaystyle = x_0 - \frac{u_0'''}{6\,k_B\,T}\,\frac{\int_{-\infty}^\infty y^4...
...y^2/(2\,k_B\,T)]\,dy}
{\int_{-\infty}^\infty \exp[-u_0''\,y^2/(2\,k_B\,T)]\,dy}$](img4109.png)

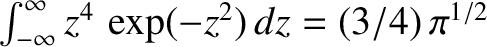 , and
, and
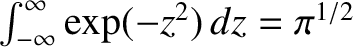 ,
so we get
,
so we get
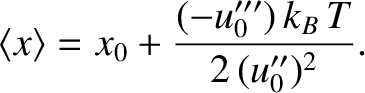
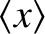 increases linearly with increasing temperature.
increases linearly with increasing temperature.
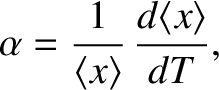
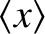 is the mean distance between nearest neighbor atoms.
The previous two equations yield
is the mean distance between nearest neighbor atoms.
The previous two equations yield
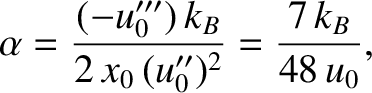
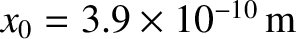 , and
, and
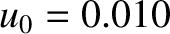 eV. Hence, we deduce
that
eV. Hence, we deduce
that
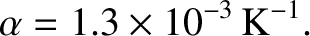
 is about
is about
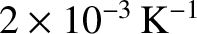 .
.