Consider a microscopic system (such as an atom) that possesses two quantum states, labelled 1 and 2.
Let the lower energy state, 1 (i.e., the ground state), have energy 0, and let the higher
energy state (i.e., the excited state), 2, have energy
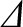 , where
, where
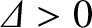 .
.
Suppose that the microscopic system is in thermal equilibrium with a heat reservoir of temperature  .
According to the Boltzmann distribution, (5.329), the probability the system is found in state
.
According to the Boltzmann distribution, (5.329), the probability the system is found in state  is
is
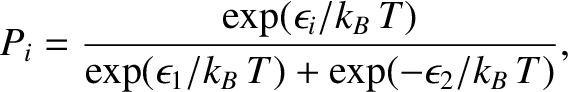 |
(5.330) |
where 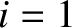 ,
, 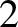 . In particular, given that
. In particular, given that
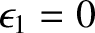 and
and
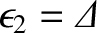 , we find
that
Note that
, we find
that
Note that 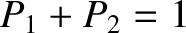 .
Thus, at low temperatures,
.
Thus, at low temperatures,
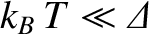 , we obtain
, we obtain
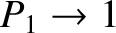 and
and
 .
In other words, at low temperatures, the system is certain to be found in its ground state, and
has no chance of being found in its excited state. On the other hand, at high temperatures,
.
In other words, at low temperatures, the system is certain to be found in its ground state, and
has no chance of being found in its excited state. On the other hand, at high temperatures,
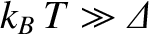 , we obtain
, we obtain
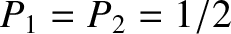 . In other words, at high temperatures, the microscopic system is equally likely
to be found in its ground state or in its excited state.
Finally, the mean energy of the microscopic system is (see Section 5.1.3)
. In other words, at high temperatures, the microscopic system is equally likely
to be found in its ground state or in its excited state.
Finally, the mean energy of the microscopic system is (see Section 5.1.3)
 |
(5.333) |
Note that there is no temperature at which its is possible to get a population inversion; that is,
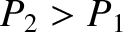 . In fact, lasers, which require a population inversion in order to operate, are not in thermal equilibrium.
. In fact, lasers, which require a population inversion in order to operate, are not in thermal equilibrium.
Figure 5.2:
Internal energy and specific heat capacity of a two-state system as a function of the temperature.
|
|
Suppose that we have a macroscopic system consisting of  identical two-state microscopic systems of the
type that we have just discussed. The internal energy of the macroscopic system is
identical two-state microscopic systems of the
type that we have just discussed. The internal energy of the macroscopic system is
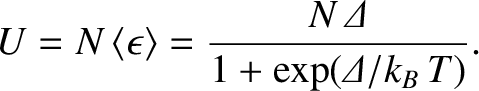 |
(5.334) |
Moreover, the specific heat capacity of the macroscopic system at constant volume is (see Section 5.2.3)
![$\displaystyle C_V = \left(\frac{\partial U}{\partial T}\right)_{V,N} = \frac{N\...
...}{k_B\,T^2}\,\frac{\exp({\mit\Delta}/k_B\,T)}{[1+\exp({\mit\Delta}/k_B\,T)]^2}.$](img4044.png) |
(5.335) |
The previous two equations yield
where
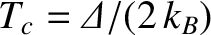 . Figure 5.2 illustrates how
. Figure 5.2 illustrates how  and
and 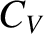 vary with temperature.
The peak in the heat capacity is known as the Schottky anomaly, and is associated with the absorption of
energy from the heat reservoir as the temperature exceeds the critical temperature required for the constituent
microscopic systems to be excited from their ground states.
vary with temperature.
The peak in the heat capacity is known as the Schottky anomaly, and is associated with the absorption of
energy from the heat reservoir as the temperature exceeds the critical temperature required for the constituent
microscopic systems to be excited from their ground states.
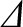 , where
, where
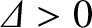 .
.
 .
According to the Boltzmann distribution, (5.329), the probability the system is found in state
.
According to the Boltzmann distribution, (5.329), the probability the system is found in state  is
is
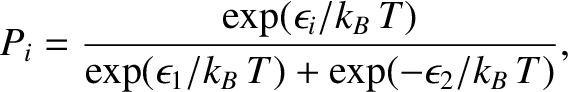
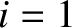 ,
, 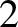 . In particular, given that
. In particular, given that
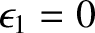 and
and
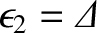 , we find
that
, we find
that
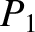
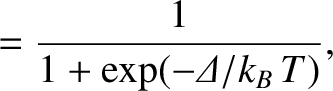
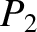

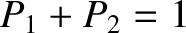 .
Thus, at low temperatures,
.
Thus, at low temperatures,
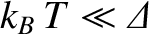 , we obtain
, we obtain
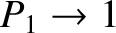 and
and
 .
In other words, at low temperatures, the system is certain to be found in its ground state, and
has no chance of being found in its excited state. On the other hand, at high temperatures,
.
In other words, at low temperatures, the system is certain to be found in its ground state, and
has no chance of being found in its excited state. On the other hand, at high temperatures,
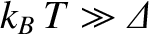 , we obtain
, we obtain
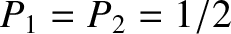 . In other words, at high temperatures, the microscopic system is equally likely
to be found in its ground state or in its excited state.
Finally, the mean energy of the microscopic system is (see Section 5.1.3)
. In other words, at high temperatures, the microscopic system is equally likely
to be found in its ground state or in its excited state.
Finally, the mean energy of the microscopic system is (see Section 5.1.3)

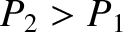 . In fact, lasers, which require a population inversion in order to operate, are not in thermal equilibrium.
. In fact, lasers, which require a population inversion in order to operate, are not in thermal equilibrium.
![\includegraphics[width=1\textwidth]{Chapter06/Figure6_1.eps}](img4042.png)
 identical two-state microscopic systems of the
type that we have just discussed. The internal energy of the macroscopic system is
identical two-state microscopic systems of the
type that we have just discussed. The internal energy of the macroscopic system is
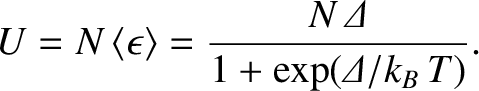
![$\displaystyle C_V = \left(\frac{\partial U}{\partial T}\right)_{V,N} = \frac{N\...
...}{k_B\,T^2}\,\frac{\exp({\mit\Delta}/k_B\,T)}{[1+\exp({\mit\Delta}/k_B\,T)]^2}.$](img4044.png)

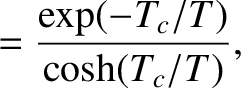
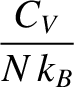

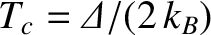 . Figure 5.2 illustrates how
. Figure 5.2 illustrates how  and
and 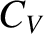 vary with temperature.
The peak in the heat capacity is known as the Schottky anomaly, and is associated with the absorption of
energy from the heat reservoir as the temperature exceeds the critical temperature required for the constituent
microscopic systems to be excited from their ground states.
vary with temperature.
The peak in the heat capacity is known as the Schottky anomaly, and is associated with the absorption of
energy from the heat reservoir as the temperature exceeds the critical temperature required for the constituent
microscopic systems to be excited from their ground states.