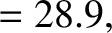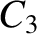Alpha Decay
Many types of heavy atomic nuclei spontaneously decay to produce daughter nuclei
via the emission of  -particles (i.e., helium nuclei) of some characteristic energy.
This process is known as
-particles (i.e., helium nuclei) of some characteristic energy.
This process is known as
 -decay. Let us investigate the
-decay. Let us investigate the  -decay of a particular type of atomic nucleus of radius
-decay of a particular type of atomic nucleus of radius  , charge-number
, charge-number 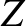 ,
and mass-number
,
and mass-number  . Such a nucleus thus decays to produce a daughter
nucleus of charge-number
. Such a nucleus thus decays to produce a daughter
nucleus of charge-number 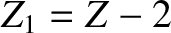 and mass-number
and mass-number 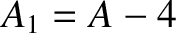 ,
and an
,
and an  -particle of charge-number
-particle of charge-number 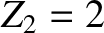 and mass-number
and mass-number
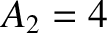 . Let the characteristic energy of the
. Let the characteristic energy of the  -particle
be
-particle
be  . Incidentally, nuclear radii
are found to satisfy the empirical formula
. Incidentally, nuclear radii
are found to satisfy the empirical formula
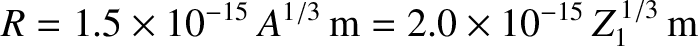 |
(4.146) |
for 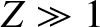 .
.
In 1928, George Gamov proposed a very successful theory of  -decay,
according to which the
-decay,
according to which the  -particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the
-particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the  -particle, whose energy is
-particle, whose energy is  , is trapped in a potential well of radius
, is trapped in a potential well of radius  by the
potential barrier
by the
potential barrier
 |
(4.147) |
for 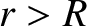 . (See Section 2.1.4.) Here,
. (See Section 2.1.4.) Here, 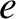 is the magnitude of the electron charge.
is the magnitude of the electron charge.
Making use of the WKB approximation (and neglecting the fact
that  is a radial, rather than a Cartesian, coordinate), the probability
of the
is a radial, rather than a Cartesian, coordinate), the probability
of the  -particle tunneling through the barrier is
-particle tunneling through the barrier is
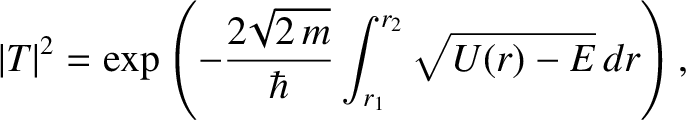 |
(4.148) |
where 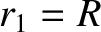 and
and
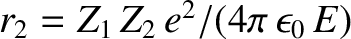 . Here,
. Here,
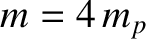 is the
is the  -particle mass, and
-particle mass, and 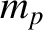 is the proton mass. The previous expression
reduces to
is the proton mass. The previous expression
reduces to
![$\displaystyle \vert T\vert^{2} = \exp\left[-2\!\sqrt{2}\,\beta \int_{1}^{E_c/E}\left(\frac{1}{y}-\frac{E}{E_c}\right)^{1/2} dy\right],$](img3225.png) |
(4.149) |
where
 |
(4.150) |
is a dimensionless constant, and
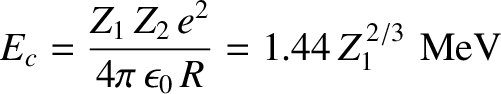 |
(4.151) |
is the characteristic energy the  -particle would need in order to escape
from the nucleus without tunneling. Of course,
-particle would need in order to escape
from the nucleus without tunneling. Of course, 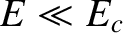 .
It is easily demonstrated that
.
It is easily demonstrated that
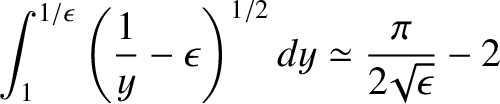 |
(4.152) |
when
 .
Hence.
.
Hence.
![$\displaystyle \vert T\vert^{2} \simeq \exp\left[-2\!\sqrt{2}\,\beta\left(\frac{\pi}{2}\!\sqrt{\frac{E_c}{E}}-2\right)\right].$](img3231.png) |
(4.153) |
Now, the  -particle moves inside the nucleus at the characteristic
velocity
-particle moves inside the nucleus at the characteristic
velocity
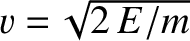 . It follows that the particle bounces backward
and forward within the nucleus at the frequency
. It follows that the particle bounces backward
and forward within the nucleus at the frequency
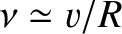 , giving
, giving
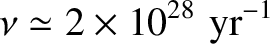 |
(4.154) |
for a 1 MeV  -particle trapped inside a typical heavy nucleus of radius
-particle trapped inside a typical heavy nucleus of radius 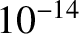 m.
Thus, the
m.
Thus, the  -particle effectively attempts to tunnel through the potential
barrier
-particle effectively attempts to tunnel through the potential
barrier 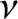 times a second. If each of these attempts has a probability
times a second. If each of these attempts has a probability
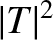 of succeeding then the probability of decay per unit time
is
of succeeding then the probability of decay per unit time
is
 . Hence, if there are
. Hence, if there are 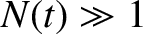 intact nuclei at time
intact nuclei at time  then
there are only
then
there are only 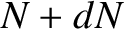 at time
at time  , where
, where
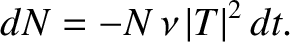 |
(4.155) |
This expression can be integrated to give
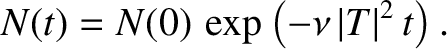 |
(4.156) |
The half-life, 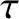 , is defined as the time which must elapse
in order for half of the nuclei originally present to decay. It follows from
the previous formula that
, is defined as the time which must elapse
in order for half of the nuclei originally present to decay. It follows from
the previous formula that
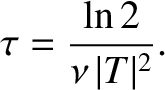 |
(4.157) |
Note that the half-life is independent of 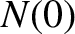 .
.
Finally, making use of the previous results, we obtain
![$\displaystyle \log_{10}[\tau ({\rm yr})] = -C_1 - C_2\,Z_1^{\,2/3} + C_3\,\frac{Z_1}{\sqrt{E({\rm MeV})}},$](img3245.png) |
(4.158) |
where
Figure: 4.12
The experimentally determined half-life,
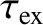 , of various atomic nuclei that decay via
, of various atomic nuclei that decay via  -emission versus the best-fit theoretical half-life
-emission versus the best-fit theoretical half-life
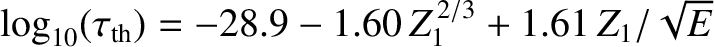 . Both half-lives are measured in years. Here,
. Both half-lives are measured in years. Here, 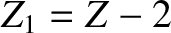 , where
, where 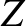 is the charge-number of the nucleus, and
is the charge-number of the nucleus, and  the characteristic energy of the emitted
the characteristic energy of the emitted  -particle in MeV. In
order of increasing half-life, the points correspond to the
following nuclei: Rn 215, Po 214, Po 216, Po 197, Fm 250, Ac 225, U 230, U 232, U 234, Gd 150, U 236, U 238, Pt 190, Gd 152, Nd 144. (Data obtained from International Atomic Energy Agency, Nuclear Data Center.)
-particle in MeV. In
order of increasing half-life, the points correspond to the
following nuclei: Rn 215, Po 214, Po 216, Po 197, Fm 250, Ac 225, U 230, U 232, U 234, Gd 150, U 236, U 238, Pt 190, Gd 152, Nd 144. (Data obtained from International Atomic Energy Agency, Nuclear Data Center.)
|
|
The half-life, 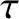 , the daughter charge-number,
, the daughter charge-number, 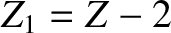 , and
the
, and
the  -particle energy,
-particle energy,  , for atomic nuclei that undergo
, for atomic nuclei that undergo  -decay
are indeed found to satisfy a relationship of the form (4.158). See Figure 4.12. The
best fit to the data shown in the figure is obtained using
-decay
are indeed found to satisfy a relationship of the form (4.158). See Figure 4.12. The
best fit to the data shown in the figure is obtained using
It can be seen that these values are remarkably similar to those calculated previously.
 -particles (i.e., helium nuclei) of some characteristic energy.
This process is known as
-particles (i.e., helium nuclei) of some characteristic energy.
This process is known as
 -decay. Let us investigate the
-decay. Let us investigate the  -decay of a particular type of atomic nucleus of radius
-decay of a particular type of atomic nucleus of radius  , charge-number
, charge-number 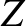 ,
and mass-number
,
and mass-number  . Such a nucleus thus decays to produce a daughter
nucleus of charge-number
. Such a nucleus thus decays to produce a daughter
nucleus of charge-number 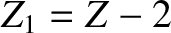 and mass-number
and mass-number 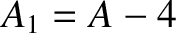 ,
and an
,
and an  -particle of charge-number
-particle of charge-number 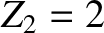 and mass-number
and mass-number
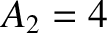 . Let the characteristic energy of the
. Let the characteristic energy of the  -particle
be
-particle
be  . Incidentally, nuclear radii
are found to satisfy the empirical formula
. Incidentally, nuclear radii
are found to satisfy the empirical formula
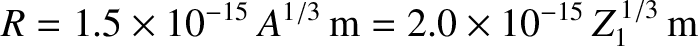
 .
.
 -decay,
according to which the
-decay,
according to which the  -particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the
-particle moves freely inside the nucleus, and is emitted after tunneling through the
potential barrier between itself and the daughter nucleus. In other words,
the  -particle, whose energy is
-particle, whose energy is  , is trapped in a potential well of radius
, is trapped in a potential well of radius  by the
potential barrier
by the
potential barrier

 . (See Section 2.1.4.) Here,
. (See Section 2.1.4.) Here, 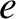 is the magnitude of the electron charge.
is the magnitude of the electron charge.
 is a radial, rather than a Cartesian, coordinate), the probability
of the
is a radial, rather than a Cartesian, coordinate), the probability
of the  -particle tunneling through the barrier is
-particle tunneling through the barrier is
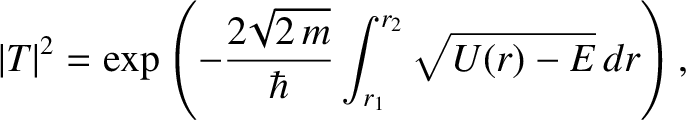
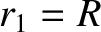 and
and
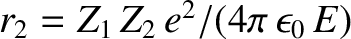 . Here,
. Here,
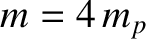 is the
is the  -particle mass, and
-particle mass, and 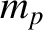 is the proton mass. The previous expression
reduces to
is the proton mass. The previous expression
reduces to
![$\displaystyle \vert T\vert^{2} = \exp\left[-2\!\sqrt{2}\,\beta \int_{1}^{E_c/E}\left(\frac{1}{y}-\frac{E}{E_c}\right)^{1/2} dy\right],$](img3225.png)

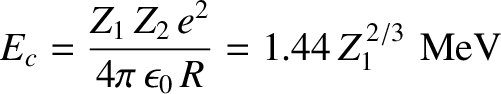
 -particle would need in order to escape
from the nucleus without tunneling. Of course,
-particle would need in order to escape
from the nucleus without tunneling. Of course,  .
It is easily demonstrated that
.
It is easily demonstrated that
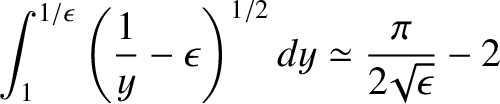
 .
Hence.
.
Hence.
![$\displaystyle \vert T\vert^{2} \simeq \exp\left[-2\!\sqrt{2}\,\beta\left(\frac{\pi}{2}\!\sqrt{\frac{E_c}{E}}-2\right)\right].$](img3231.png)
 -particle moves inside the nucleus at the characteristic
velocity
-particle moves inside the nucleus at the characteristic
velocity
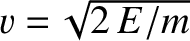 . It follows that the particle bounces backward
and forward within the nucleus at the frequency
. It follows that the particle bounces backward
and forward within the nucleus at the frequency
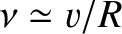 , giving
, giving
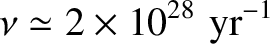
 -particle trapped inside a typical heavy nucleus of radius
-particle trapped inside a typical heavy nucleus of radius 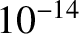 m.
Thus, the
m.
Thus, the  -particle effectively attempts to tunnel through the potential
barrier
-particle effectively attempts to tunnel through the potential
barrier 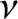 times a second. If each of these attempts has a probability
times a second. If each of these attempts has a probability
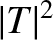 of succeeding then the probability of decay per unit time
is
of succeeding then the probability of decay per unit time
is
 . Hence, if there are
. Hence, if there are 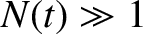 intact nuclei at time
intact nuclei at time  then
there are only
then
there are only 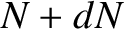 at time
at time  , where
, where
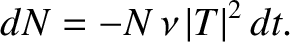
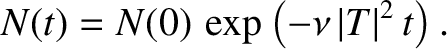
 , is defined as the time which must elapse
in order for half of the nuclei originally present to decay. It follows from
the previous formula that
, is defined as the time which must elapse
in order for half of the nuclei originally present to decay. It follows from
the previous formula that
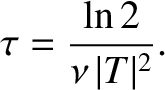
 .
.



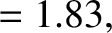
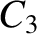
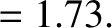
![\includegraphics[width=0.85\textwidth]{Chapter05/fig11_13.eps}](img3252.png)
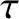 , the daughter charge-number,
, the daughter charge-number, 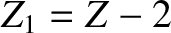 , and
the
, and
the  -particle energy,
-particle energy,  , for atomic nuclei that undergo
, for atomic nuclei that undergo  -decay
are indeed found to satisfy a relationship of the form (4.158). See Figure 4.12. The
best fit to the data shown in the figure is obtained using
-decay
are indeed found to satisfy a relationship of the form (4.158). See Figure 4.12. The
best fit to the data shown in the figure is obtained using