


Next: Irrotational Flow
Up: Incompressible Inviscid Flow
Previous: Circulation and Vorticity
Kelvin Circulation Theorem
According to the Kelvin circulation theorem, which is named after Lord Kelvin (1824-1907), the
circulation around any co-moving loop in an
inviscid fluid is independent of time. The
proof is as follows. The circulation around a given loop  is defined
is defined
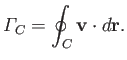 |
(4.78) |
However, for a loop that is co-moving with the fluid, we have
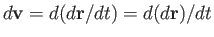 . Thus,
. Thus,
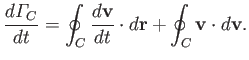 |
(4.79) |
By definition,
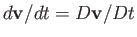 for a co-moving loop. (See Section 1.10.) Moreover, the equation of motion of
an incompressible inviscid fluid can be written [see Equation (1.79)]
for a co-moving loop. (See Section 1.10.) Moreover, the equation of motion of
an incompressible inviscid fluid can be written [see Equation (1.79)]
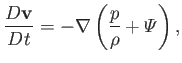 |
(4.80) |
because  is a constant. Hence,
is a constant. Hence,
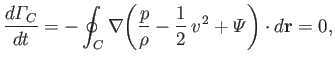 |
(4.81) |
because
 (see Section A.18), and
(see Section A.18), and
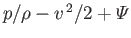 is obviously a single-valued function.
is obviously a single-valued function.
Figure 4.10:
A vortex tube.
 |
One corollary of the Kelvin circulation theorem is that the fluid particles that form the walls of a vortex tube at a given instance in time continue to
form the walls of a vortex tube at all subsequent times. To prove this, imagine a closed loop  that is embedded in the wall of a vortex tube but does
not circulate around the interior of the tube. (See Figure 4.10.) The normal component of the
vorticity over the surface enclosed by
that is embedded in the wall of a vortex tube but does
not circulate around the interior of the tube. (See Figure 4.10.) The normal component of the
vorticity over the surface enclosed by  is zero, because all vorticity vectors are tangential to this surface.
Thus, from Equation (4.77), the circulation around the loop is zero. By Kelvin's circulation theorem, the circulation around the loop remains zero as the
tube is convected by the fluid. In other words, although the
surface enclosed by
is zero, because all vorticity vectors are tangential to this surface.
Thus, from Equation (4.77), the circulation around the loop is zero. By Kelvin's circulation theorem, the circulation around the loop remains zero as the
tube is convected by the fluid. In other words, although the
surface enclosed by  deforms, as it is convected by the fluid, it always remains on the tube wall, because
no vortex filaments can pass through it.
deforms, as it is convected by the fluid, it always remains on the tube wall, because
no vortex filaments can pass through it.
Another corollary of the circulation theorem is that the intensity of a vortex tube remains constant as it
is convected by the fluid. This can be proved by considering the circulation around the loop  pictured
in Figure 4.10.
pictured
in Figure 4.10.



Next: Irrotational Flow
Up: Incompressible Inviscid Flow
Previous: Circulation and Vorticity
Richard Fitzpatrick
2016-03-31
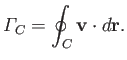
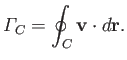
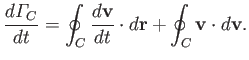
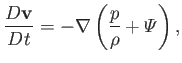
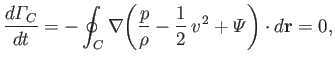
![]() that is embedded in the wall of a vortex tube but does
not circulate around the interior of the tube. (See Figure 4.10.) The normal component of the
vorticity over the surface enclosed by
that is embedded in the wall of a vortex tube but does
not circulate around the interior of the tube. (See Figure 4.10.) The normal component of the
vorticity over the surface enclosed by ![]() is zero, because all vorticity vectors are tangential to this surface.
Thus, from Equation (4.77), the circulation around the loop is zero. By Kelvin's circulation theorem, the circulation around the loop remains zero as the
tube is convected by the fluid. In other words, although the
surface enclosed by
is zero, because all vorticity vectors are tangential to this surface.
Thus, from Equation (4.77), the circulation around the loop is zero. By Kelvin's circulation theorem, the circulation around the loop remains zero as the
tube is convected by the fluid. In other words, although the
surface enclosed by ![]() deforms, as it is convected by the fluid, it always remains on the tube wall, because
no vortex filaments can pass through it.
deforms, as it is convected by the fluid, it always remains on the tube wall, because
no vortex filaments can pass through it.
![]() pictured
in Figure 4.10.
pictured
in Figure 4.10.