

Next: Gravity Waves at an
Up: Waves in Incompressible Fluids
Previous: Ship Wakes
Consider a gravity wave traveling through a fluid that is flowing horizontally at the uniform velocity
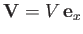 . Let us write
. Let us write
where 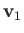 and
and 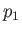 are the small velocity and pressure perturbations, respectively, due to the wave.
To first order in small quantities, the fluid equations of motion, (11.1) and (11.2),
reduce to
are the small velocity and pressure perturbations, respectively, due to the wave.
To first order in small quantities, the fluid equations of motion, (11.1) and (11.2),
reduce to
respectively.
We can also define the displacement,
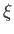
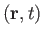 , of a fluid particle due to the passage of the wave, as seen in a frame co-moving with the fluid, as
, of a fluid particle due to the passage of the wave, as seen in a frame co-moving with the fluid, as
The curl of Equation (11.87) implies that
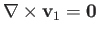 . Hence, we can write
. Hence, we can write
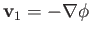 , and
Equation (11.87) yields
, and
Equation (11.87) yields
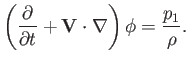 |
(11.89) |
Finally, Equation (11.86) gives
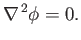 |
(11.90) |
The most general traveling wave solution to Equation (11.90), with wave vector
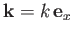 , and angular frequency
, and angular frequency 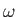 , is
, is
![$\displaystyle \phi(x,z,t)= \left[A\,\cosh(k\,z)+B\,\sinh(k\,z)\right]\cos(\omega\,t-k\,x).$](img4079.png) |
(11.91) |
It follows from Equation (11.89) that
![$\displaystyle p_1(x,z,t) = \rho\,k\,(V-c)\left[A\,\cosh(k\,z) + B\,\sinh(k\,z)\right]\sin(\omega\,t-k\,x),$](img4080.png) |
(11.92) |
and from Equation (11.88) that
![$\displaystyle \xi_z(x,z,t,) = (V-c)^{-1}\left[A\,\sinh(k\,z)+ B\,\cosh(k\,z)\right]\sin(\omega\,t-k\,x).$](img4081.png) |
(11.93) |
Here,
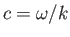 is the phase velocity of the wave.
is the phase velocity of the wave.


Next: Gravity Waves at an
Up: Waves in Incompressible Fluids
Previous: Ship Wakes
Richard Fitzpatrick
2016-03-31
![]() . Hence, we can write
. Hence, we can write
![]() , and
Equation (11.87) yields
, and
Equation (11.87) yields
![]() , and angular frequency
, and angular frequency ![]() , is
, is