


Next: Steady Flow over a
Up: Waves in Incompressible Fluids
Previous: Gravity Waves in a
Consider a layer of fluid of density 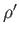 , depth
, depth  , and uniform horizontal velocity
, and uniform horizontal velocity 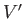 , situated on top of a layer of another fluid of density
, situated on top of a layer of another fluid of density  ,
depth
,
depth  , and uniform horizontal velocity
, and uniform horizontal velocity  . Suppose that the fluids are bounded from above and below by rigid horizontal planes. Let these
planes lie at
. Suppose that the fluids are bounded from above and below by rigid horizontal planes. Let these
planes lie at 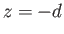 and
and  , and let the unperturbed interface between the two fluids lie at
, and let the unperturbed interface between the two fluids lie at  . (See Figure 11.8.)
. (See Figure 11.8.)
Figure 11.8:
Gravity waves at an interface between two immiscible fluids.
 |
Consider a gravity wave of angular frequency  , and wavenumber
, and wavenumber 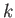 , propagating through both fluids in the
, propagating through both fluids in the  -direction.
Let
-direction.
Let
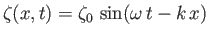 |
(11.94) |
be the small vertical displacement of the interface due to the wave. In the lower fluid, the perturbed velocity potential must be of the form (11.91),
with the constants  and
and 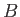 chosen such that
chosen such that
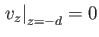 and
and
 . It follows
that
. It follows
that
 and
and
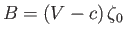 , so that
, so that
![$\displaystyle \phi(x,z,t) = (V-c)\,\zeta_0\,\frac{\cosh[k\,(z+d)]}{\sinh(k\,d)}\,\cos(\omega\,t-k\,x).$](img4093.png) |
(11.95) |
In the upper fluid, the perturbed velocity potential must again be of the form (11.91),
with the constants  and
and 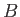 chosen such that
chosen such that
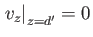 and
and
 . It follows
that
. It follows
that
 and
and
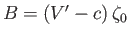 , so that
, so that
![$\displaystyle \phi(x,z,t) = -(V'-c)\,\zeta_0\,\frac{\cosh[k\,(z-d')]}{\sinh(k\,d')}\,\cos(\omega\,t-k\,x).$](img4097.png) |
(11.96) |
Here,
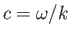 is the phase velocity of the wave.
From Equations (11.85) and (11.92), the fluid pressure just below the interface is
is the phase velocity of the wave.
From Equations (11.85) and (11.92), the fluid pressure just below the interface is
Likewise, the fluid pressure just above the interface is
In the absence of surface tension at the interface, these two pressure must equal one another: that is,
![$\displaystyle \left[p\right]_{z=0_-}^{z=0_+}=0.$](img4106.png) |
(11.99) |
Hence, we
obtain the dispersion relation
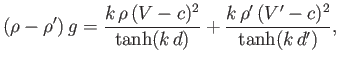 |
(11.100) |
which takes the form of a quadratic equation for the phase velocity, 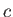 , of the wave.
We can see that:
, of the wave.
We can see that:
- If
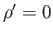 and
and  then the dispersion relation reduces to (11.43) (with
then the dispersion relation reduces to (11.43) (with 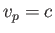 ).
).
- If the two fluids are of infinite depth then the dispersion relation simplifies to
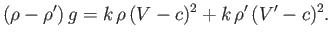 |
(11.101) |
- In general, there are two values of
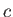 that satisfy the quadratic equation (11.100). These are either both real, or form a complex conjugate pair.
that satisfy the quadratic equation (11.100). These are either both real, or form a complex conjugate pair.
- The condition for stability is that
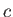 is real. The alternative is that
is real. The alternative is that 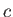 is complex, which implies that
is complex, which implies that  is also complex, and,
hence,
that the perturbation grows or decays exponentially in time. Because the complex roots of a quadratic equation occur in complex
conjugate pairs, one of the roots always corresponds to an exponentially growing mode. In other words, an instability.
is also complex, and,
hence,
that the perturbation grows or decays exponentially in time. Because the complex roots of a quadratic equation occur in complex
conjugate pairs, one of the roots always corresponds to an exponentially growing mode. In other words, an instability.
- If both fluids are at rest (i.e.,
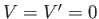 ), and of infinite depth, then the dispersion reduces to
), and of infinite depth, then the dispersion reduces to
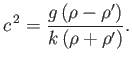 |
(11.102) |
It follows that the configuration is only stable when
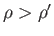 : that is, when the heavier fluid is underneath.
: that is, when the heavier fluid is underneath.
As a particular example, suppose that the lower fluid is water, and the upper fluid is the atmosphere. Let
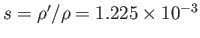 be the specific
density of air at s.t.p. (relative to water). Putting
be the specific
density of air at s.t.p. (relative to water). Putting 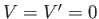 ,
,
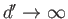 ,
and making use of the fact that
,
and making use of the fact that 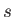 is small, the dispersion relation (11.100) yields
is small, the dispersion relation (11.100) yields
![$\displaystyle c\simeq (g\,d)^{1/2}\left[\frac{\tanh(k\,d)}{k\,d}\right]^{1/2}\left\{1-\frac{1}{2}\,s\,[1+\tanh(k\,d)]\right\}.$](img4117.png) |
(11.103) |
Comparing this with Equation (11.43), we can see that the presence of the atmosphere tends to slightly diminish the phase velocities of gravity waves propagating over the
surface of a body of water.



Next: Steady Flow over a
Up: Waves in Incompressible Fluids
Previous: Gravity Waves in a
Richard Fitzpatrick
2016-03-31

![]() , and wavenumber
, and wavenumber ![]() , propagating through both fluids in the
, propagating through both fluids in the ![]() -direction.
Let
-direction.
Let
![$\displaystyle \phi(x,z,t) = (V-c)\,\zeta_0\,\frac{\cosh[k\,(z+d)]}{\sinh(k\,d)}\,\cos(\omega\,t-k\,x).$](img4093.png)
![$\displaystyle \phi(x,z,t) = -(V'-c)\,\zeta_0\,\frac{\cosh[k\,(z-d')]}{\sinh(k\,d')}\,\cos(\omega\,t-k\,x).$](img4097.png)
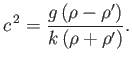
![]() be the specific
density of air at s.t.p. (relative to water). Putting
be the specific
density of air at s.t.p. (relative to water). Putting ![]() ,
,
![]() ,
and making use of the fact that
,
and making use of the fact that ![]() is small, the dispersion relation (11.100) yields
is small, the dispersion relation (11.100) yields
![$\displaystyle c\simeq (g\,d)^{1/2}\left[\frac{\tanh(k\,d)}{k\,d}\right]^{1/2}\left\{1-\frac{1}{2}\,s\,[1+\tanh(k\,d)]\right\}.$](img4117.png)